题目内容
已知椭圆C:x2+2y2=4.则椭圆C的离心率是 .
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:第一步:将椭圆方程化为标准形式:
+
=1(a、b>0);
第二步:根据a>b,得a2,b2,由c2=a2-b2,得c2;
第三步:由离心率的定义e=
,即可得椭圆的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
第二步:根据a>b,得a2,b2,由c2=a2-b2,得c2;
第三步:由离心率的定义e=
| c |
| a |
解答:
解:将x2+2y2=4化为
+
=1.
则a2=4,b2=2,
从而c2=a2-b2=4-2=2,
所以椭圆C的离心率c=
=
=
.
故答案为:
.
| x2 |
| 4 |
| y2 |
| 2 |
则a2=4,b2=2,
从而c2=a2-b2=4-2=2,
所以椭圆C的离心率c=
| c |
| a |
| ||
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题属容易题,考查了椭圆离心率的求法.若已知椭圆的方程,一般是先求得a,c,直接利用离心率的定义求解,求解时应注意以下几点:
①在椭圆的标准方程
+
=1中,分母较大的是a2,分母较小的是b2;②关系式“a2=b2+c2”可实现a,b,c之间的转换,不要错记成“c2=a2+b2”;
③求得的离心率e,其值在区间(0,1)内.
①在椭圆的标准方程
| x2 |
| a2 |
| y2 |
| b2 |
③求得的离心率e,其值在区间(0,1)内.

练习册系列答案
相关题目
从空间一点P向二面角α-l-β的两个半平面α,β分别作垂线PE,PF,垂足分别为E,F,若二面角α-l-β的大小为60°,则<
,
>的大小为( )
| PF |
| PE |
| A、30°或150° |
| B、120° |
| C、60°或120° |
| D、60° |
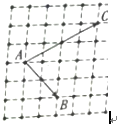 如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.
如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.