题目内容
(文)(1)设命题p:若a≥0,则x2+x-a=0有实根.试写出命题p的逆否命题并判断真假;
(2)设命题p:函数y=kx+1在R上是增函数,命题q:曲线y=x2+(2k-3)x+1与x轴交于不同的两点,如果p∧q是真命题,求k的取值范围.
(2)设命题p:函数y=kx+1在R上是增函数,命题q:曲线y=x2+(2k-3)x+1与x轴交于不同的两点,如果p∧q是真命题,求k的取值范围.
考点:复合命题的真假,四种命题
专题:简易逻辑
分析:(1)根据逆否命题的定义和关系即可得到结论;
(2)若p∧q是真命题,则等价为p,q都是真命题,进行判断求解即可.
(2)若p∧q是真命题,则等价为p,q都是真命题,进行判断求解即可.
解答:
解:(1)设命题p的逆否命题为:若x2+x-a=0无实根,则a<0.
若方程无实数根,则判别式△=1+4a<0,解得a<-
,故a<0成立,逆否命题为真命题.
(2)∵p∧q是真命题,∴p,q都是真命题,
若函数y=kx+1在R上是增函数,则k>0,
若y=x2+(2k-3)x+1与x轴交于不同的两点,则(2k-3)2-4>0,
解得k>
或k<
,
故k的取值范围是k>
或0<k<
.
若方程无实数根,则判别式△=1+4a<0,解得a<-
| 1 |
| 4 |
(2)∵p∧q是真命题,∴p,q都是真命题,
若函数y=kx+1在R上是增函数,则k>0,
若y=x2+(2k-3)x+1与x轴交于不同的两点,则(2k-3)2-4>0,
解得k>
| 5 |
| 2 |
| 1 |
| 2 |
故k的取值范围是k>
| 5 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查四种命题之间的关系以及复合命题之间的应用.根据命题关系求出对应的等价条件是解决本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知如图所示的程序框图,当输入n=99时,输出S的值( )


A、
| ||
B、
| ||
C、
| ||
D、
|
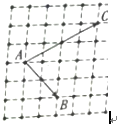 如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.
如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.