题目内容
20．一面积为$\frac{3\sqrt{3}}{2}$cm2的正六边形的六个顶点都在球O的表面上，球心O到正六边形所在平面的距离为2$\sqrt{2}$cm，记球O的体积为Vcm3，球O的表面积为Scm2，则（ ）| A． | V=S | B． | V=2S | C． | 2V=S | D． | V=$\sqrt{2}$S |
分析 利用面积为$\frac{3\sqrt{3}}{2}$cm2的正六边形，求出正六边形的边长，可得正六边形所在小圆的半径，即可求出球O的半径，从而可得结论．
解答 解：设正六边形的边长为a，则$\frac{\sqrt{3}}{4}{a}^{2}×6$=$\frac{3\sqrt{3}}{2}$，∴a=1，
∴正六边形所在小圆的半径为r=1，
∴球O的半径为R=$\sqrt{8+1}$=3，
∴$\frac{V}{S}$=$\frac{R}{3}$=1．
故选：A．
点评 本题考查球O的体积与表面积，考查学生的计算能力，确定球O的半径是关键．
练习册系列答案
阅读快车系列答案
相关题目
12．
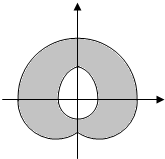如图是集合P={（x，y）|（x-cosθ）2+（y-sinθ）2=4，0≤θ≤π}中的点在平面上运动时留下的阴影，中间形如“水滴”部分的平面面积为（ ）
如图是集合P={（x，y）|（x-cosθ）2+（y-sinθ）2=4，0≤θ≤π}中的点在平面上运动时留下的阴影，中间形如“水滴”部分的平面面积为（ ）| A． | $\frac{11}{6}π-\sqrt{3}$ | B． | $\frac{7}{3}π-\sqrt{3}$ | C． | $π+\sqrt{3}$ | D． | π+2 |