题目内容
10.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是不共线的非零向量,且$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$.(1)已知$\overrightarrow{c}$=3$\overrightarrow{{e}_{1}}$+4$\overrightarrow{{e}_{2}}$,以$\overrightarrow{a}$,$\overrightarrow{b}$为基底,表示向量$\overrightarrow{c}$;
(2)若4$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$,求λ,μ的值.
分析 根据平面向量的基本定理分别列出方程组解出;
解答 解:(1)设$\overrightarrow{c}=λ\overrightarrow{a}+μ\overrightarrow{b}$,则3$\overrightarrow{{e}_{1}}$+4$\overrightarrow{{e}_{2}}$=λ($\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$)+μ($\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=(λ+μ)$\overrightarrow{{e}_{1}}$+(3μ-2λ)$\overrightarrow{{e}_{2}}$.
∴$\left\{\begin{array}{l}{λ+μ=3}\\{3μ-2λ=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{λ=1}\\{μ=2}\end{array}\right.$,∴$\overrightarrow{c}$=$\overrightarrow{a}+2\overrightarrow{b}$.
(2)4$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$=λ($\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$)+μ($\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=(λ+μ)$\overrightarrow{{e}_{1}}$+(3μ-2λ)$\overrightarrow{{e}_{2}}$.
∴$\left\{\begin{array}{l}{λ+μ=4}\\{3μ-2λ=-3}\end{array}\right.$,解得λ=3,μ=1.
点评 本题考查了平面向量的基本定理及其应用,属于基础题.

| A. | V=S | B. | V=2S | C. | 2V=S | D. | V=$\sqrt{2}$S |
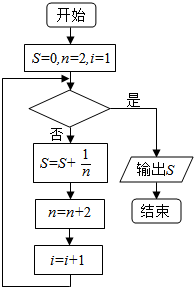 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( ) 一只受伤的丹顶鹤在如图所示(直角梯形)的草原上飞过,其中AD=$\sqrt{2}$,DC=2,BC=1,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是1-$\frac{π}{10}$.
一只受伤的丹顶鹤在如图所示(直角梯形)的草原上飞过,其中AD=$\sqrt{2}$,DC=2,BC=1,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是1-$\frac{π}{10}$. 已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条
已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条