题目内容
在古希腊，毕达哥拉斯学派把1，3，5，10，15，…这些数叫做三角形数，这是因为这些数目的点可以排成正三角形（如图所示），如图所示，则第七个三角形数是（ ）
| A、30 | B、29 | C、28 | D、27 |
考点：归纳推理
专题：计算题,推理和证明
分析：原来三角形数是从l开始的连续自然数的和．l是第一个三角形数，3是第二个三角形数，6是第三个三角形数，10是第四个三角形数，15是第五个三角形数…那么，第七个三角形数就是：l+2+3+4+5+6+7=28．
解答：
解：原来三角形数是从l开始的连续自然数的和．
l是第一个三角形数，
3是第二个三角形数，
6是第三个三角形数，
10是第四个三角形数，
15是第五个三角形数，
…
那么，第七个三角形数就是：l+2+3+4+5+6+7=28．
故选：C．
l是第一个三角形数，
3是第二个三角形数，
6是第三个三角形数，
10是第四个三角形数，
15是第五个三角形数，
…
那么，第七个三角形数就是：l+2+3+4+5+6+7=28．
故选：C．
点评：本题考查数列在生产实际中的应用，考查运算求解能力，推理论证能力；考查化归与转化思想．综合性强，难度大，易出错，是高考的重点．解题时要认真审题，注意总结规律．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
把函数y=sin（2x+
）的图象向左平移
个单位，再把图象上所有的点的横坐标扩大为原来的2倍，纵坐标缩短为原来的
倍；然后把图象向下平移2个单位．最后得到的函数解析式为：（ ）
| π |
| 3 |
| π |
| 12 |
| 1 |
| 3 |
A、y=
| ||||
| B、y=3cos4x+2 | ||||
C、y=
| ||||
D、y=3sin（4x+
|
点A，B，C，D均在同一球面上，且AB、AC、AD两两垂直，且AB=1，AC=2，AD=3，则该球的表面积为（ ）
| A、7π | ||||
| B、14π | ||||
C、
| ||||
D、
|
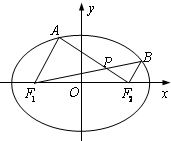如图，在平面直角坐标系xoy中，椭圆| x2 |
| 2 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
F为抛物线y2=2px （p＞0）的焦点，过点F的直线与该抛物线交于A，B两点，l1，l2分别是该抛物线在A，B两点处的切线，l1，l2相交于点C，设|AF|=a，|BF|=b，则|CF|=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的程序框图，如果输入的t∈[-3，3]，则输出的S属于（ ）
| A、[-6，2] |
| B、[-3，16] |
| C、[-4，5] |
| D、[-6，0] |
若f（x）=
，则f（x）的定义域为（ ）
| 1 | ||||
|
A、（-
| ||
| B、（-1，0） | ||
C、（-
| ||
| D、（0，+∞） |
等比数列{an}前n项和为Sn，q=3，则
=（ ）
| S4 |
| a4 |
A、
| ||
B、
| ||
C、
| ||
D、
|