题目内容
已知在△ABC中，两中线AD、BE互相垂直，求
+
．
| tanC |
| tanA |
| tanC |
| tanB |
考点：解三角形
专题：解三角形
分析：设出三角形的三条边长，利用中点得到BD=CD=
，AE=EC=
，DE=
AB=
．然后由直角三角形中的余弦定理得到5c2=a2+b2．把要求解的式子先化切为弦，然后结合正弦定理和余弦定理得答案．
| a |
| 2 |
| b |
| 2 |
| 1 |
| 2 |
| c |
| 2 |
解答：
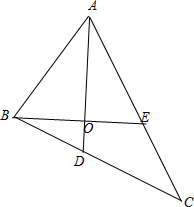解：如图，
△ABC中，设BC=a，AC=b，AB=c，
∵AD⊥BE，∴∠BOA=90°，
又D与E分别为BC，AC的中点，
∴BD=CD=
，AE=EC=
．
DE=
AB=
．
①在Rt△BOD中，BO2+DO2=(
)2．
②在Rt△AOE中，AO2+EO2=(
)2．
③在Rt△EOD中，DO2+EO2=(
)2．
④在Rt△AOB中，BO2+AO2=c2．
由①+②=③+④得：5c2=a2+b2．
∴
+
=tanC•
=tanC•
=
．
由正弦定理得：
=
，
∴上式=
=
=
．
解：如图，△ABC中，设BC=a，AC=b，AB=c，
∵AD⊥BE，∴∠BOA=90°，
又D与E分别为BC，AC的中点，
∴BD=CD=
| a |
| 2 |
| b |
| 2 |
DE=
| 1 |
| 2 |
| c |
| 2 |
①在Rt△BOD中，BO2+DO2=(
| a |
| 2 |
②在Rt△AOE中，AO2+EO2=(
| b |
| 2 |
③在Rt△EOD中，DO2+EO2=(
| c |
| 2 |
④在Rt△AOB中，BO2+AO2=c2．
由①+②=③+④得：5c2=a2+b2．
∴
| tanC |
| tanA |
| tanC |
| tanB |
| sinBcosA+sinAcosB |
| sinAsinB |
=tanC•
| sin(A+B) |
| sinAsinB |
| sin2C |
| sinAsinBcosC |
由正弦定理得：
| sin2C |
| sinAsinB |
| c2 |
| ab |
∴上式=
| c2 |
| ab•cosC |
| c2 | ||
ab•
|
| 1 |
| 2 |
点评：本题考查了三角形的解法，考查了正弦定理和余弦定理的应用，解答此题的关键在于由已知得到a，b，c的关系式，是中档题．
练习册系列答案
相关题目
若在甲袋内装有8个白球，4个红球，在乙袋内装有6个白球，6个红球，今从两袋里面各任意取出1个球，设取去的白球的个数为ξ，则下列概率中等于
的是（ ）
| ||||||||
|
| A、P（ξ=0） |
| B、P（ξ≤2） |
| C、P（ξ=1） |
| D、P（ξ=2） |