题目内容
2．焦点在x轴上，长、短半轴长之和为10，焦距为$4\sqrt{5}$，则椭圆的标准方程为（ ）| A． | $\frac{x^2}{6}+\frac{y^2}{4}=1$ | B． | $\frac{x^2}{16}+\frac{y^2}{36}=1$ | C． | $\frac{x^2}{36}+\frac{y^2}{16}=1$ | D． | $\frac{x^2}{49}+\frac{y^2}{9}=1$ |
分析 利用椭圆的简单性质列出方程，求解即可．
解答 解：焦点在x轴上，长、短半轴长之和为10，焦距为$4\sqrt{5}$，
可得a+b=10，2c=4$\sqrt{5}$，c=2$\sqrt{5}$，即a2-b2=20，
解得a2=36，b2=16，
所求椭圆方程为：$\frac{x^2}{36}+\frac{y^2}{16}=1$．
故选：C．
点评 本题考查椭圆的简单性质的应用，椭圆方程的求法，考查计算能力．
练习册系列答案
名师点拨卷系列答案
相关题目
12．已知在△ABC中，∠ACB=$\frac{π}{2}$，AB=2BC，现将△ABC绕BC所在直线旋转到△PBC，设二面角P-BC-A大小为θ，PB与平面ABC所成角为α，PC与平面PAB所成角为β，若0＜θ＜π，则（ ）
| A． | $α≤\frac{π}{3}$且$sinβ≤\frac{{\sqrt{3}}}{3}$ | B． | $α≤\frac{π}{3}$且$sinβ＜\frac{{\sqrt{3}}}{3}$ | C． | $α≤\frac{π}{6}$且$β≥\frac{π}{3}$ | D． | $α≤\frac{π}{6}$且$β＜\frac{π}{3}$ |
13．设函数f（x）是定义在R上的奇函数，则下列结论中一定正确的是（ ）
| A． | 函数f（x）+x2是奇函数 | B． | 函数f（x）+|x|是偶函数 | ||
| C． | 函数x2f（x）是奇函数 | D． | 函数|x|f（x）是偶函数 |
10．已知命题p：?x∈R，sinx≤1，则￢p为（ ）
| A． | ?x∈R，sinx≤1 | B． | ?x∈R，sinx＞1 | C． | ?x∈R，sinx≥1 | D． | ?x∈R，sinx＞1 |
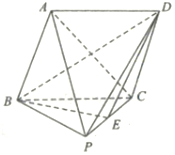如图，在四棱锥P-ABCD中，底面ABCD是菱形，侧面PBC是直角三角形，∠PCB=90°，点E是PC的中点，且平面PBC⊥平面ABCD．
11．若双曲线$\frac{x^2}{3}-{y^2}=1$的左焦点在抛物线y2=2px的准线上，则p的值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | $4\sqrt{2}$ |
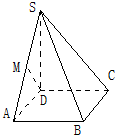如图，四棱锥S-ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，SD=1，SB=$\sqrt{3}$．