题目内容
17.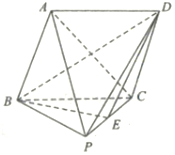 如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.求证:
(1)AP∥平面BED;
(2)BD⊥平面APC.
分析 (1)取AC,BD的交点O,连结OE,根据中位线定理得出OE∥AP,故而AP∥平面BDE;
(2)由平面PBC⊥平面ABCD得出PC⊥平面ABCD,故而PC⊥BD,由菱形性质得出BD⊥AC,即可证明BD⊥平面PAC.
解答 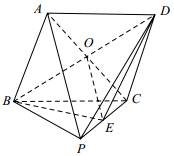 解:(1)设AC∩BD=O,连结OE.因为ABCD是菱形,
解:(1)设AC∩BD=O,连结OE.因为ABCD是菱形,
所以O为AC的中点.
又因为点E是PC的中点,
所以OE是△APC的中位线.
所以AP∥OE.
又OE?平面BED,AP?平面BED,
所以AP∥平面BED.
注:不写条件OE?平面BED,AP?平面BED,各扣 1 分.
(2)因为平面PBC⊥平面ABCD,PC?平面PBC,平面PBC∩平面ABCD=BC,PC⊥BC,
所以PC⊥平面ABCD,
所以PC⊥BD.
因为底面ABCD是菱形,
所以BD⊥AC.
又AC∩PC=C,
所以BD⊥平面APC.
点评 本题考查了线面平行的判定,线面垂直的性质与判定,考查了数形结合思想和空间想象能力以及推理论证能力,属于中档题.

练习册系列答案
相关题目
7.已知直线l1:x-y+1=0和l2:x-y+3=0,则l1与l2之间距离是( )
| A. | $2\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
2.焦点在x轴上,长、短半轴长之和为10,焦距为$4\sqrt{5}$,则椭圆的标准方程为( )
| A. | $\frac{x^2}{6}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{36}=1$ | C. | $\frac{x^2}{36}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{49}+\frac{y^2}{9}=1$ |
19. 一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )
一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )
 一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )
一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )| A. | 2$\sqrt{3}$ | B. | 12 | C. | 2$\sqrt{3}$+12 | D. | 2$\sqrt{3}$+6 |
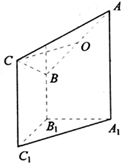 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.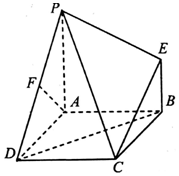 如图,四边形ABCD是正方形,PA⊥平面ABCD,EB∥PA,AB=PA=4,EB=2,F为PD的中点.
如图,四边形ABCD是正方形,PA⊥平面ABCD,EB∥PA,AB=PA=4,EB=2,F为PD的中点.