题目内容
已知圆C的圆心在坐标原点O,且与直线l1:x-y-2
=0相切.
(1)求直线l2:4x-3y+5=0被圆C所截得的弦AB的长;
(2)若与直线l1垂直的直线与圆C交于不同的两点P,Q,且以PQ为直径的圆过原点,求直线的纵截距;
(3)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N,求直线MN的方程.
| 2 |
(1)求直线l2:4x-3y+5=0被圆C所截得的弦AB的长;
(2)若与直线l1垂直的直线与圆C交于不同的两点P,Q,且以PQ为直径的圆过原点,求直线的纵截距;
(3)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N,求直线MN的方程.
考点:直线与圆的位置关系,圆的切线方程
专题:综合题,直线与圆
分析:(1)先求出圆C的标准方程,再求直线l2:4x-3y+5=0被圆C所截得的弦AB的长;
(2)设直线的方程为:y=-x+b联立x2+y2=4,利用x1x 2+y1y2=2x1x 2-b(x1+x2)+b2=0,即可求直线的纵截距;
(3)求出以G点为圆心,线段GM长为半径的圆G方程,与圆C的标准方程相减,即可求直线MN的方程.
(2)设直线的方程为:y=-x+b联立x2+y2=4,利用x1x 2+y1y2=2x1x 2-b(x1+x2)+b2=0,即可求直线的纵截距;
(3)求出以G点为圆心,线段GM长为半径的圆G方程,与圆C的标准方程相减,即可求直线MN的方程.
解答:
解:(1)由题意得:圆心(0,0)到直线l1:x-y-2
=0的距离为圆的半径,r=
=2,
所以圆C的标准方程为:x2+y2=4(2分)
所以圆心到直线l2的距离d=
=1(3分)
∴|AB|=2
=2
(4分)
(2)设直线的方程为:y=-x+b联立x2+y2=4得:2x2-2bx+b2-4=0,
设直线与圆的交点P(x1,y1),Q(x2,y2),
由△=(-2b)2-8(b2-4)>0,得b2<8,x1+x2=b,x1•x2=
①(10分)
因为OP⊥OQ,所以
•
=0,即满足x1x2+y1y2=0,
又y1=-x1+b,y2=-x2+b,
所以x1x 2+y1y2=2x1x 2-b(x1+x2)+b2=0②
由①②得b2=4,满足△>0,即b=2或-2(9分)
(3)因为点G(1,3),所以|OG|=
=
,|GM|=
=
所以以G点为圆心,线段GM长为半径的圆G方程:(x-1)2+(y-3)2=6③
又圆C方程为:x2+y2=4④,由③-④得直线MN方程:x+3y-4=0(14分)
| 2 |
2
| ||
| 2 |
所以圆C的标准方程为:x2+y2=4(2分)
所以圆心到直线l2的距离d=
| 22-3 |
∴|AB|=2
| 22-12 |
| 3 |
(2)设直线的方程为:y=-x+b联立x2+y2=4得:2x2-2bx+b2-4=0,
设直线与圆的交点P(x1,y1),Q(x2,y2),
由△=(-2b)2-8(b2-4)>0,得b2<8,x1+x2=b,x1•x2=
| b2-4 |
| 2 |
因为OP⊥OQ,所以
| OP |
| OQ |
又y1=-x1+b,y2=-x2+b,
所以x1x 2+y1y2=2x1x 2-b(x1+x2)+b2=0②
由①②得b2=4,满足△>0,即b=2或-2(9分)
(3)因为点G(1,3),所以|OG|=
| 12+32 |
| 10 |
| OG2-OM2 |
| 6 |
所以以G点为圆心,线段GM长为半径的圆G方程:(x-1)2+(y-3)2=6③
又圆C方程为:x2+y2=4④,由③-④得直线MN方程:x+3y-4=0(14分)
点评:本题考查圆的方程,考查直线与圆的位置关系,考查圆与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)是定义在(-6,6)上的偶函数,f(x)在[0,6]上是单调函数,且f(-2)≤f(1),f(-2)=25,那么下列肯定不正确的是( )
| A、f(1)≥25 |
| B、f(2)=25 |
| C、f(1)<25 |
| D、f(1)>25 |
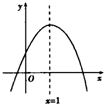 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论: