题目内容
在△ABC中,若B=60°,AB=2,AC=2
,则△ABC的面积( )
| 3 |
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:利用正弦定理列出关系式,把AB,AC,sinB的值代入求出sinC的值,确定出C的度数,进而求出A的度数,利用三角形面积公式求出三角形ABC面积即可.
解答:
解:∵在△ABC中,B=60°,AB=2,AC=2
,
∴由正弦定理
=
得:sinC=
=
=
,
∴C=30°,
∴A=90°,
则S△ABC=
AB•AC•sinA=2
,
故选:B.
| 3 |
∴由正弦定理
| AC |
| sinB |
| AB |
| sinC |
| ABsinB |
| AC |
2×
| ||||
2
|
| 1 |
| 2 |
∴C=30°,
∴A=90°,
则S△ABC=
| 1 |
| 2 |
| 3 |
故选:B.
点评:此题考查了正弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
已知x>0,y>0,x+3y+3xy=8,则x+3y的最小值是( )
A、
| ||
| B、5 | ||
C、
| ||
| D、4 |
已知f(
)=x-2
,则f(x)=( )
| x+2 |
| x+2 |
| A、f(x)=x2-2x-2(x≥-2) |
| B、f(x)=x2-2x-2(x≥0) |
| C、f(x)=x2-2x+2(x≥-2) |
| D、f(x)=x2-2x+2(x≥0) |
某中学高中学生有900名.为了考察他们的体重状况,打算抽取容量为45的一个样本.已知高一有400名学生,高二有300名学生,高三有200名学生.若采取分层抽样的办法抽取,则高一学生需要抽取的学生个数为( )
| A、20人 | B、15人 |
| C、10人 | D、5人 |
若集合A={x|y=
},且A∩B=B,则集合B可能是( )
| x |
| A、{1,2,3} |
| B、{x|-1<x<1} |
| C、{-2,2} |
| D、R |
函数y=
的定义域为( )
| ||
| x |
| A、[-1,0) |
| B、(0,+∞) |
| C、[-1,0)∪(0,+∞) |
| D、(-∞,0)∪(0,+∞) |
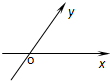 如图,在平面斜坐标系中∠xOy=60°,平面上任意一点P的斜坐标是这样定义的:若
如图,在平面斜坐标系中∠xOy=60°,平面上任意一点P的斜坐标是这样定义的:若| OP |
| e1 |
| e2 |
| e1 |
| e2 |
| A、x2+y2=2 |
| B、x2+y2=4 |
| C、x2+y2+xy=2 |
| D、x2+y2+xy=4 |