题目内容

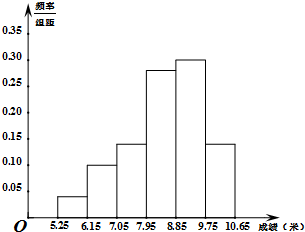某市为了了解今年高中毕业生的体能情况，从本市某高中毕业班中抽取了一个班进行铅球测试，成绩在8.0米（精确到0.1米）以上的为合格，把所得数据进行整理后，分成六组画出频率分布直方图的一部分，如图，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第六小组的频数是7．
（1）求这次铅球测试成绩合格的人数；
（2）若从第一小组和第二小组中随机抽取两个人的测试成绩，则两个人的测试成绩来自同一小组的概率是多少？
考点：古典概型及其概率计算公式,频率分布直方图
专题：计算题,概率与统计
分析：（1）利用频率和为1求出第六组的频率；利用频率等于频数除以样本容量求出此次测试总人数．
（2）确定基本事件的个数，利用古典概型概率公式求解即可．
解答： 解：（1）第6小组的频率为：1-（0.04+0.10+0.14+0.28+0.30）=0.14
则此次测试总人数为50人，又第四、五、六组成绩均合格，所以合格的人数为
50（0.28+0.30+0.14）=36人 （4分）
（2）由已知可知第一组含两个样本，第二组含5个样本，将第一组的学生成绩编号为（a1，a2），
将第二组的学生成绩编号为（b1，b2，b3，b4，b5），从一二组中随机取两个元素的基本事件空间Ω中共有21个元素，而且这些基本事件出现时等可能的．
用A表示“两个元素来自同一组”这一事件，则A里包含的基本事件有11个，
∴P(A)=
11
21
，
答：所求事件概率为
11
21
（12分）
点评：本小题主要考查统计与概率的相关知识，具体涉及到频率分布直方图、中位数及古典概型等内容．
练习册系列答案
相关题目
从装有n+1个球的口袋中取出m个球（0＜m≤n，m，n∈N），共有C
 
m
n+1
种取法．在这C
 
m
n+1
种取法中，可以分成一个指定的球被取到和未被取到两类：一类是该指定的球未被取到，共有C
 
0
1
•C
 
m
n
种取法；另一类是该指定的球被取到，共有C
 
1
1
•C
 
m-1
n
种取法．显然C10•Cnm+C11•Cnm-1=C
 
m
n+1
，即有等式：C
 
m
n
+C
 
m-1
n
=C
 
m
n+1
成立．试根据上述思想，则有：Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k（其中当1≤k＜m≤n，k，m，n∈N）为（　　）
A、C
 
m
n+k
B、C
 
m
n+k+1
C、C
 
m+1
n+k
D、C
 
k
n+m
下面多面体中有12条棱的是（　　）
A、四棱柱B、四棱锥
C、五棱锥D、五棱柱
一批手机成箱包装，每箱5只，某客户在购进这批手机之前，首先取出3箱，再从每箱中任取2只手机进行检验．设3箱手机中有二等品依次为0、1、2只，其余都是一等品．
（Ⅰ）用X表示抽检的6只手机中二等品的件数，求X的分布列和数学期望；
（Ⅱ）若抽检的6只手机中有2只或2只以上的为二等品，用户就拒绝购买这批手机，求用户拒绝购买这批手机的概率．
在平面直角坐标系xOy中，点A（1，-2），B（a，-1），C（-b，0），且a＞0，b＞0．
（1）若点A，B，C在直线L上，求u=
1
a
+
2
b
的最小值，并求此时直线L的方程；
（2）若以线段AB，AC为邻边的平行四边形的两条对角线的长相等，且
OA
•（
AB
-
AC
）=5 求a，b的值．
在数列{an}中，a1=1，对任意的正整数n，都有（1-an+1）（2+an）=2，且an≠0．
（Ⅰ）求证：{
1
an
+1}是等比数列；
（Ⅱ）求数列{
n
an
}的前n项和．
设数列{an}的前n项和为Sn，a1=10，an+1=9Sn+10．
（Ⅰ）求证：{lgan}是等差数列；
（Ⅱ）设Tn是数列{
3
(lgan)(lgan+1)
}的前n项和，求Tn；
（Ⅲ）求使Tn＞
1
4
（m2-5m）对所有的n∈N*恒成立的整数m的取值集合．
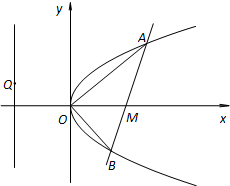已知直线l过点M（4，0）且与抛物线y2=2px（p＞0）交于A、B两点，以弦AB为直径的圆恒过坐标原点O．
（Ⅰ）求抛物线的标准方程；
（Ⅱ）设Q是直线x=-4上任意一点，求证：直线QA、QM、QB的斜率依次成等差数列．
已知a，b，c∈R+，且
a
1+a
+
b
1+b
+
c
1+c
=1，求证：a+b+c≥
3
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网