题目内容
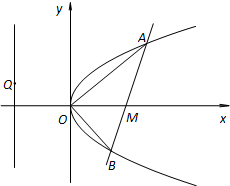 已知直线l过点M(4,0)且与抛物线y2=2px(p>0)交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
已知直线l过点M(4,0)且与抛物线y2=2px(p>0)交于A、B两点,以弦AB为直径的圆恒过坐标原点O.(Ⅰ)求抛物线的标准方程;
(Ⅱ)设Q是直线x=-4上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设直线l方程为x=ky+4,代入y2 =2px,得y2-2kpy-8p=0,由此利用韦达定理、向量的数量积结合已知条件能求出抛物线方程.
(Ⅱ)设Q(-4,t)由(Ⅰ)知y1+y2=4k,y1y2=-16,由此能推导出KQA+KQB=
+
=-
=2KQM,从而得到直线QA、QP、QB的斜率依次成等差数列.
(Ⅱ)设Q(-4,t)由(Ⅰ)知y1+y2=4k,y1y2=-16,由此能推导出KQA+KQB=
| 4(y1-t) | ||
|
| 4(y2-t) | ||
|
| t |
| 4 |
解答:
(Ⅰ)解:∵直线l过点M(4,0),
∴设直线l方程为x=ky+4,
代入y2 =2px,得y2-2kpy-8p=0,
设A(x1,y1),B(x2,y2),
则y1+y2=2kp,y1 y2 =-8p,…(2分)^^
∵
•
=0,
∴0=x1x2+y1y2=(ky1+4)(ky2+4)-8p
=k2y1y2+4k(y1+y2)+16-8p,
即0=-8k2p+8k2p+16-8p,解得p=2,
∴抛物线方程为y2=4x.…(6分)
(Ⅱ)证明:设Q(-4,t)由(Ⅰ)知y1+y2=4k,y1y2=-16,
∴
+
=(y1+y2)2-2y1y2=16k2+32,
∵KQA=
=
=
,
KQB=
=
=
,KQM=
…(9分)
KQA+KQB=
+
=4×
=4×
=
=
=-
=2KQM…(12分)
即直线QA、QP、QB的斜率依次成等差数列.…(13分)
∴设直线l方程为x=ky+4,
代入y2 =2px,得y2-2kpy-8p=0,
设A(x1,y1),B(x2,y2),
则y1+y2=2kp,y1 y2 =-8p,…(2分)^^
∵
| OA |
| OB |
∴0=x1x2+y1y2=(ky1+4)(ky2+4)-8p
=k2y1y2+4k(y1+y2)+16-8p,
即0=-8k2p+8k2p+16-8p,解得p=2,
∴抛物线方程为y2=4x.…(6分)
(Ⅱ)证明:设Q(-4,t)由(Ⅰ)知y1+y2=4k,y1y2=-16,
∴
| y | 2 1 |
| y | 2 2 |
∵KQA=
| y1-t |
| x1+4 |
| y1-t | ||||
|
| 4(y1-t) | ||
|
KQB=
| y2-t |
| x2+4 |
| y2-t | ||||
|
| 4(y2-t) | ||
|
| t |
| -8 |
KQA+KQB=
| 4(y1-t) | ||
|
| 4(y2-t) | ||
|
=4×
(y1-t)(
| ||||
(
|
=4×
y1
| ||||||||
|
=
-t(
| ||||
8×16+4(
|
| -t(16k2+32)-32t |
| 8×16+4(16k2+32) |
=-
| t |
| 4 |
即直线QA、QP、QB的斜率依次成等差数列.…(13分)
点评:本题考查抛物线方程的求法,考查直线QA、QM、QB的斜率依次成等差数列的证明,解题时要认真审题,注意向量知识的灵活运用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
设f(x)=x2+ax+b(a,b∈R),当x∈[-1,1]时,|f(x)|的最大值为m,则m的最小值为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
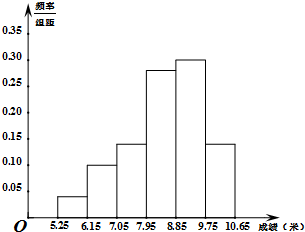 某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.
某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7. 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=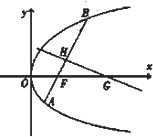 已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.
已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.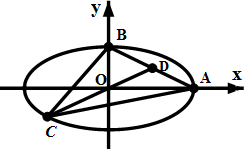 如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为
如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为