题目内容
设数列{an}的前n项和为Sn,a1=10,an+1=9Sn+10.
(Ⅰ)求证:{lgan}是等差数列;
(Ⅱ)设Tn是数列{
}的前n项和,求Tn;
(Ⅲ)求使Tn>
(m2-5m)对所有的n∈N*恒成立的整数m的取值集合.
(Ⅰ)求证:{lgan}是等差数列;
(Ⅱ)设Tn是数列{
| 3 |
| (lgan)(lgan+1) |
(Ⅲ)求使Tn>
| 1 |
| 4 |
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(I)根据等差数列的定义即可证明{lgan}是等差数列;
(Ⅱ)求出{
}的通项公式,利用裂项法即可求Tn;
(Ⅲ)直接解不等式即可得到结论.
(Ⅱ)求出{
| 3 |
| (lgan)(lgan+1) |
(Ⅲ)直接解不等式即可得到结论.
解答:
解:(I)∵a1=10,an+1=9Sn+10.
∴当n=1时,a2=9a1+10=100,
故
=10,
当n≥1时,an+1=9Sn+10 ①,
an+2=9Sn+1+10 ②,
两式相减得an+2-an+1=9an+1,
即an+2=10an+1,
即
=10,
即{an}是首项a1=10,公比q=10的等比数列,
则数列{an}的通项公式an=10•10n-1=10n;
则lgan=lg10n=n,
则lgan-lgan-1=n-(n-1)=1,为常数,
即{lgan}是等差数列;
(Ⅱ)∵lgan=n,则
=
=3(
-
),
则Tn=3(1-
+
-
+…+
-
)=3(1-
)=3-
,
(Ⅲ)∵Tn=3-
≥T1=
,
∴要使Tn>
(m2-5m)对所有的n∈N*恒成立,
则
>
(m2-5m)对所有的n∈N*恒成立,
解得-1<m<6,
故整数m的取值集合{0,1,2,3,4,5}.
∴当n=1时,a2=9a1+10=100,
故
| a2 |
| a1 |
当n≥1时,an+1=9Sn+10 ①,
an+2=9Sn+1+10 ②,
两式相减得an+2-an+1=9an+1,
即an+2=10an+1,
即
| an+2 |
| an+1 |
即{an}是首项a1=10,公比q=10的等比数列,
则数列{an}的通项公式an=10•10n-1=10n;
则lgan=lg10n=n,
则lgan-lgan-1=n-(n-1)=1,为常数,
即{lgan}是等差数列;
(Ⅱ)∵lgan=n,则
| 3 |
| (lgan)(lgan+1) |
| 3 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则Tn=3(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 3 |
| n+1 |
(Ⅲ)∵Tn=3-
| 3 |
| n+1 |
| 3 |
| 2 |
∴要使Tn>
| 1 |
| 4 |
则
| 3 |
| 2 |
| 1 |
| 4 |
解得-1<m<6,
故整数m的取值集合{0,1,2,3,4,5}.
点评:本题主要考查等差数列的判断,利用裂项法求和,考查学生的运算能力.

练习册系列答案
相关题目
函数f(x)=
-2sinπx(-2≤x≤4)所有零点之和等于( )
| 1 |
| x-1 |
| A、2 | B、4 | C、6 | D、8 |
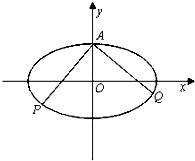 已知左焦点为F1(-2
已知左焦点为F1(-2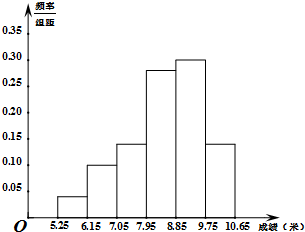 某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.
某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7. 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=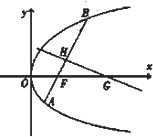 已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.
已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.