题目内容
在数列{an}中,a1=1,对任意的正整数n,都有(1-an+1)(2+an)=2,且an≠0.
(Ⅰ)求证:{
+1}是等比数列;
(Ⅱ)求数列{
}的前n项和.
(Ⅰ)求证:{
| 1 |
| an |
(Ⅱ)求数列{
| n |
| an |
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)根据等比数列的定义,即可证明{
+1}是等比数列;
(Ⅱ)利用错位相减法即可求数列{
}的前n项和.
| 1 |
| an |
(Ⅱ)利用错位相减法即可求数列{
| n |
| an |
解答:
解:(Ⅰ)∵(1-an+1)(2+an)=2,
∴an-2an+1-anan+1=0,
即
-
=1,
即
+1=2(
+1),
又
+1=2,
∴{
+1}是首项为2,公比q=2的等比数列;
(Ⅱ)∵{
+1}是首项为2,公比q=2的等比数列;
∴
+1=2•2n-1=2n,
即
=2n-1,则
=n(2n-1),
则数列{
}的前n项和Sn=2-1+2(2n-1)+…+n(2n-1)=(2+2×22+…+n×2n)-(1+2+…+n),
设T=2+2×22+…+n×2n,
则2T=22+2×23+…+n×2n+1,
∴-T=2+22+23+…-n×2n+1=(1-n)×2n+1-2,
即T=(n-1)2n+1+2,
∴Sn=(n-1)2n+1+2-
.
∴an-2an+1-anan+1=0,
即
| 1 |
| an+1 |
| 2 |
| an |
即
| 1 |
| an+1 |
| 1 |
| an |
又
| 1 |
| a1 |
∴{
| 1 |
| an |
(Ⅱ)∵{
| 1 |
| an |
∴
| 1 |
| an |
即
| 1 |
| an |
| n |
| an |
则数列{
| n |
| an |
设T=2+2×22+…+n×2n,
则2T=22+2×23+…+n×2n+1,
∴-T=2+22+23+…-n×2n+1=(1-n)×2n+1-2,
即T=(n-1)2n+1+2,
∴Sn=(n-1)2n+1+2-
| n(n+1) |
| 2 |
点评:本题主要考查等比数列的判断和证明,要求熟练掌握错位相减法.考查学生的计算能力.

练习册系列答案
相关题目
记A=cos
,B=cos
,C=sin
-sin
,则A,B,C的大小关系是( )
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| A、A>B>C |
| B、A>C>B |
| C、B>A>C |
| D、C>B>A |
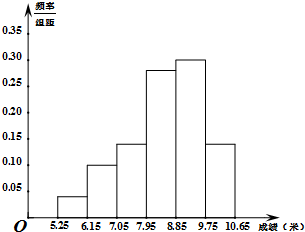 某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.
某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7. 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=