题目内容
已知a,b,c∈R+,且
+
+
=1,求证:a+b+c≥
.
| a |
| 1+a |
| b |
| 1+b |
| c |
| 1+c |
| 3 |
| 2 |
考点:反证法与放缩法
专题:证明题,不等式的解法及应用
分析:令x=
,y=
,z=
,则x+y+z=1,x,y,z∈R+,a=
,b=
,c=
,可得a+b+c=
+
+
=
+
+
-3,利用基本不等式,即可证明结论.
| a |
| 1+a |
| b |
| 1+b |
| c |
| 1+c |
| x |
| y+z |
| y |
| x+z |
| z |
| x+y |
| x |
| y+z |
| y |
| x+z |
| z |
| x+y |
| 1 |
| y+z |
| 1 |
| x+z |
| 1 |
| x+y |
解答:
证明:令x=
,y=
,z=
,则x+y+z=1,x,y,z∈R+.
∴a=
,b=
,c=
,
∴a+b+c=
+
+
=
+
+
-3,
∵
+
+
≥3
,
(y+z)+(x+z)+(x+y)≥3
,
∴两式相乘可得2(
+
+
)≥9,
∴
+
+
≥
,
∴a+b+c≥
-3=
.
| a |
| 1+a |
| b |
| 1+b |
| c |
| 1+c |
∴a=
| x |
| y+z |
| y |
| x+z |
| z |
| x+y |
∴a+b+c=
| x |
| y+z |
| y |
| x+z |
| z |
| x+y |
| 1 |
| y+z |
| 1 |
| x+z |
| 1 |
| x+y |
∵
| 1 |
| y+z |
| 1 |
| x+z |
| 1 |
| x+y |
| 3 |
| ||||||
(y+z)+(x+z)+(x+y)≥3
| 3 | (y+z)(x+z)(x+y) |
∴两式相乘可得2(
| 1 |
| y+z |
| 1 |
| x+z |
| 1 |
| x+y |
∴
| 1 |
| y+z |
| 1 |
| x+z |
| 1 |
| x+y |
| 9 |
| 2 |
∴a+b+c≥
| 9 |
| 2 |
| 3 |
| 2 |
点评:本题考查不等式的证明,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
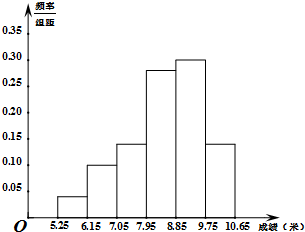 某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.
某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.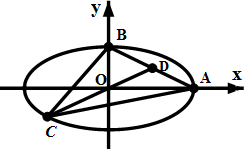 如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为
如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为