题目内容

一批手机成箱包装，每箱5只，某客户在购进这批手机之前，首先取出3箱，再从每箱中任取2只手机进行检验．设3箱手机中有二等品依次为0、1、2只，其余都是一等品．
（Ⅰ）用X表示抽检的6只手机中二等品的件数，求X的分布列和数学期望；
（Ⅱ）若抽检的6只手机中有2只或2只以上的为二等品，用户就拒绝购买这批手机，求用户拒绝购买这批手机的概率．
考点：古典概型及其概率计算公式,离散型随机变量的期望与方差
专题：应用题,概率与统计
分析：（Ⅰ）由取出的第一、二、三箱中分别有0件、1件、2件二等品可知变量X的取值，结合变量对应的事件做出这四个事件发生的概率，写出分布列和期望．
（Ⅱ）由上一问做出的分布列可以知道，P（X=2），P（X=3），这两个事件是互斥的，根据互斥事件的概率公式得到结果．
解答： 解：（Ⅰ）X可能的取值为0，1，2，3．
P（X=0）=
C
2
4
C
2
5
•
C
2
3
C
2
5
=
9
50
；P（X=1）=
C
2
4
C
2
5
•
C
1
2
C
1
3
C
2
5
+
C
1
4
C
2
5
•
C
2
3
C
2
5
=
12
15
；
P（X=2）=
C
1
4
C
2
5
•
C
1
2
C
1
3
C
2
5
+
C
2
4
C
2
5
•
C
2
2
C
2
5
=
3
10
；P（X=3）=
C
1
4
C
2
5
•
C
2
2
C
2
5
=
1
25

X的分布列为
X 0 1 2 3
P
9
50
12
15
3
10
1
25
EEX=0×
9
50
+1×
12
15
+2×
3
10
+3×
1
25
=
6
5
；
（Ⅱ）所求的概率为P（X≥2）=P（X=2）+P（X=3）=
3
10
+
1
25
=
17
50
．
点评：本题主要考查分布列的求法以及利用分布列求期望和概率，求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题，题目做起来不难，运算量也不大．
练习册系列答案
相关题目
cos（-1560°）的值为（　　）
A、-
1
2
B、
1
2
C、-
3
2
D、
3
2
设f（x）=x2+ax+b（a，b∈R），当x∈[-1，1]时，|f（x）|的最大值为m，则m的最小值为（　　）
A、
1
2
B、1
C、
3
2
D、2
设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）过点（1，
3
2
），F1、F2分别为椭圆C的左、右两个焦点，且离心率e=
1
2
．
（1）求椭圆C的方程；
（2）已知O为坐标原点，直线l过椭圆的右焦点F2与椭圆C交于M、N两点．若OM、ON 的斜率k1，k2满足k1+k2=-3，求直线l的方程．
已知左焦点为F1（-2
2
，0）的椭圆过点（
3
2
2
，
2
2
），过上顶点A作两条互相垂直的动弦AP，AQ交椭圆于P，Q两点．
（1）求椭圆的标准方程；
（2）若动弦AP所在直线的斜率为1，求直角三角形APQ的面积；
（3）试问动直线PQ是否过定点？若过定点，请给出证明，并求出该定点；若不过定点，请说明理由．
由-1，0，1，2，3这五个数中选三个不同的数组成二次函数y=a2x+bx+c的系数．
（1）开口向下的抛物线有几条？
（2）开口向上且不过原点的抛物线有多少条？
（3）与x轴的正、负半轴各有一个交点的抛物线有多少条？
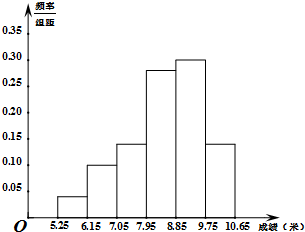某市为了了解今年高中毕业生的体能情况，从本市某高中毕业班中抽取了一个班进行铅球测试，成绩在8.0米（精确到0.1米）以上的为合格，把所得数据进行整理后，分成六组画出频率分布直方图的一部分，如图，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第六小组的频数是7．
（1）求这次铅球测试成绩合格的人数；
（2）若从第一小组和第二小组中随机抽取两个人的测试成绩，则两个人的测试成绩来自同一小组的概率是多少？
如图，ABCD是边长为2的正方形，ED⊥平面ABCD，ED=1，EF∥BD且EF=
1
2
BD
（1）求证：BF∥平面ACE；
（2）求二面角B-AF-C的大小；
（3）求点F到平面ACE的距离．
已知函数f（x）定义在R上，对任意的x，y∈R，f（x）≠0，且f（x+y）=f（x）f（y）．
（Ⅰ）求f（0），并证明：f（x-y）=
f(x)
f(y)
；
（Ⅱ）若f（x）单调，且f（1）=2．设向量
a
=（
2
cos
θ
2
，1），
b
=（
2
λsin
θ
2
，cos2θ），对任意θ∈[0，2π），f（
a
•
b
）-f（3）≤0恒成立，求实数λ的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网