题目内容
在平面直角坐标系xOy中,点A(1,-2),B(a,-1),C(-b,0),且a>0,b>0.
(1)若点A,B,C在直线L上,求u=
+
的最小值,并求此时直线L的方程;
(2)若以线段AB,AC为邻边的平行四边形的两条对角线的长相等,且
•(
-
)=5 求a,b的值.
(1)若点A,B,C在直线L上,求u=
| 1 |
| a |
| 2 |
| b |
(2)若以线段AB,AC为邻边的平行四边形的两条对角线的长相等,且
| OA |
| AB |
| AC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)根据若A,B,C在直线L上,利用向量共线可以得到a,b的一个方程,u的最小值可以利用基本不等式求解,等号成立的条件又可得到一个a,b的方程,联立可求出a,b,进而利用两点式写出直线L的方程;
(2)由条件得AB⊥AC,利用向量的内积为0可得到a,b的一个方程,再利用
•(
-
)=5,代入坐标得到一个关于a,b的方程,联立可解出a,b.
(2)由条件得AB⊥AC,利用向量的内积为0可得到a,b的一个方程,再利用
| OA |
| AB |
| AC |
解答:
解:(1)若A,B,C在直线L上,
∵
=(a-1,1),
=(-b-1,2)
∴(a-1)×2-(-b-1)×1=0
即2a+b=1,
∵a>0,b>0,u=
+
=(
+
)×(2a+b)=
+
+4≥8,
当且仅当
=
时等号成立,即2a=b,
∵2a+b=1,∴a=
,b=
∴u的最小值为8,
∴由两点式得:
=
,整理得:4x+3y+2=0.
∴直线L的方程为:4x+3y+2=0.
(2)由条件得AB⊥AC,所以
•
=0,
而
=(a-1,1),
=(-b-1,2)
∴ab+a-b-3=0,-----------①
又
•(
-
)=5,∴a+b-3=0,------②
由①②得,a=2,b=1或a=3,b=0(舍去)
∴a=2,b=1.
∵
| AB |
| AC |
∴(a-1)×2-(-b-1)×1=0
即2a+b=1,
∵a>0,b>0,u=
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 4a |
| b |
当且仅当
| b |
| a |
| 4a |
| b |
∵2a+b=1,∴a=
| 1 |
| 4 |
| 1 |
| 2 |
∴u的最小值为8,
∴由两点式得:
| y-(-2) |
| 0-(-2) |
| x-1 | ||
-
|
∴直线L的方程为:4x+3y+2=0.
(2)由条件得AB⊥AC,所以
| AB |
| AC |
而
| AB |
| AC |
∴ab+a-b-3=0,-----------①
又
| OA |
| AB |
| AC |
由①②得,a=2,b=1或a=3,b=0(舍去)
∴a=2,b=1.
点评:本题考查了向量的运算及应用,以及求最值的方法,主要考查了方程思想,根据条件运用向量的坐标运算构建方程组是解决本题的关键.

练习册系列答案
相关题目
在各棱长都相等的三棱锥A-BCD中,二面角A-BC-D的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| 3 |
| i |
| A、-3i | ||
B、-
| ||
| C、i | ||
| D、-i |
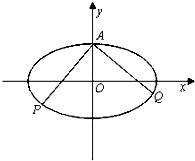 已知左焦点为F1(-2
已知左焦点为F1(-2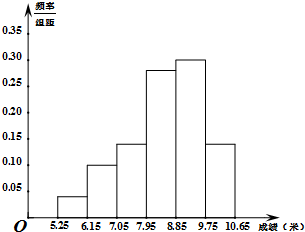 某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.
某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.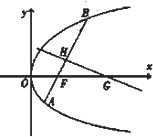 已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.
已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.