题目内容
从装有n+1个球的口袋中取出m个球(0<m≤n,m,n∈N),共有C
种取法.在这C
种取法中,可以分成一个指定的球被取到和未被取到两类:一类是该指定的球未被取到,共有C
•C
种取法;另一类是该指定的球被取到,共有C
•C
种取法.显然C10•Cnm+C11•Cnm-1=C
,即有等式:C
+C
=C
成立.试根据上述思想,则有:Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k(其中当1≤k<m≤n,k,m,n∈N)为( )
m n+1 |
m n+1 |
0 1 |
m n |
1 1 |
m-1 n |
m n+1 |
m n |
m-1 n |
m n+1 |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
考点:进行简单的合情推理
专题:规律型
分析:从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有Cn+1m种取法.在这Cn+1m种取法中,可以分成两类:一类是取出的m个球全部为白球,另一类是,取出1个黑球,m-1个白球,则Cnm+Cnm-1=Cn+1m根据上述思想,在式子:Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k中,从第一项到最后一项分别表示:从装有n个白球,k个黑球的袋子里,取出m个球的所有情况取法总数的和,故答案应为:从从装有n+k球中取出m个球的不同取法数,根据排列组合公式,可得答案.
解答:
解:在Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k中,
从第一项到最后一项分别表示:
从装有n个白球,k个黑球的袋子里,
取出m个球的所有情况取法总数的和,
故答案应为:从从装有n+k球中取出m个球的不同取法数Cn+km
故选:A
从第一项到最后一项分别表示:
从装有n个白球,k个黑球的袋子里,
取出m个球的所有情况取法总数的和,
故答案应为:从从装有n+k球中取出m个球的不同取法数Cn+km
故选:A
点评:这个题结合考查了推理和排列组合,处理本题的关键是熟练掌握排列组合公式,明白每一项所表示的含义,再结合已知条件进行分析,最后给出正确的答案.

练习册系列答案
相关题目
己知
,
是夹角为60°的两个单位向量,则
=2
+
模是( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| A、3 | ||
B、
| ||
C、
| ||
| D、7 |
方程x2+(k-2)x+5-k=0的两个不等实根都大于2,则实数k的取值范围是( )
| A、k<-2 |
| B、k≤-4 |
| C、-5<k≤-4 |
| D、-5<k<-4 |
cos(-1560°)的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在各棱长都相等的三棱锥A-BCD中,二面角A-BC-D的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
记A=cos
,B=cos
,C=sin
-sin
,则A,B,C的大小关系是( )
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| A、A>B>C |
| B、A>C>B |
| C、B>A>C |
| D、C>B>A |
函数f(x)=
-2sinπx(-2≤x≤4)所有零点之和等于( )
| 1 |
| x-1 |
| A、2 | B、4 | C、6 | D、8 |
设f(x)=x2+ax+b(a,b∈R),当x∈[-1,1]时,|f(x)|的最大值为m,则m的最小值为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
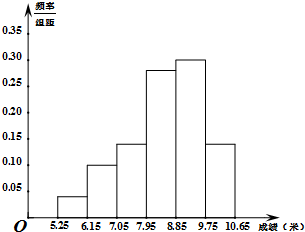 某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.
某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.