题目内容
已知集合A={x∈Z|x2-2x≤0}，集合B={x|x=2a，a∈A}，则A∩B为（ ）
| A、{0} | B、{2} |
| C、{0，2} | D、{1，4} |
考点：交集及其运算
专题：集合
分析：利用交集性质求解．
解答：
解：∵集合A={x∈Z|x2-2x≤0}={0，1，2}，
集合B={x|x=2a，a∈A}={0，2，4}，
∴A∩B={0，2}．
故选：C．
集合B={x|x=2a，a∈A}={0，2，4}，
∴A∩B={0，2}．
故选：C．
点评：本题考查交集的求法，解题时要认真审题，是基础题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
命题“存在x1∈R，3 x1≤0”的否定是（ ）
| A、对任意的x∈R，3x＞0 |
| B、对任意的x∈R，3x≤0 |
| C、不存在x1∈R，3 x1＞0 |
| D、存在x1∈R，3 x1≥0 |
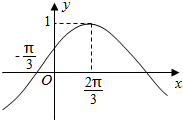已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（
| ||||
C、f（x）=sin（
| ||||
D、f（x）=sin（
|
设函数f（x）在R上单调递减，且对于任意实数m，n，总有f（m+n）=f（m）•f（n），设A={（x，y）|f（x2）•f（y2）＞f（1）}，B={（x，y）|f（ax-y+2）=1，a∈R}，若A∩B=∅，则a的取值范围是（ ）
A、-
| ||||
B、-
| ||||
C、0≤a≤
| ||||
D、-
|
要得到函数f（x）=-
f（
-x）-sinx的图象，只需将g（x）=sinx的图象（ ）
| 3 |
| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知c＞0，设p：函数f（x）=cx在R上单调递减，q：函数g（x）=
的定义域是R，如果“p且q”是假命题，“p或q”是真命题，那么c的取值范围是（ ）
| 1 |
| 2cx2+2x+1 |
A、（
| ||
B、（
| ||
C、（0，
| ||
D、（0，
|
i是虚数单位，
=（ ）
| 3i |
| 2-i |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
设全集U={0，1，2，3，4，5，6，7，8，9}，集合A={1，2，3，4，5}，集合B={1，3，5，7，9}，则∁UA∩∁UB为（ ）
| A、{6，8} |
| B、{0，6，8} |
| C、{1，3，5} |
| D、{1，2，3，4，5，7，9} |