题目内容
已知函数f(x)=
x3+
mx2+nx+2;
(1)如果函数f(x)有两个极值点-1和2,求实数m、n的值;
(2)若函数f(x)有两个极值点x1和x2,且x1∈[-1,1],x2∈[1,+∞],求(m-2)2+(n-1)2的最小值.
| 1 |
| 3 |
| 1 |
| 2 |
(1)如果函数f(x)有两个极值点-1和2,求实数m、n的值;
(2)若函数f(x)有两个极值点x1和x2,且x1∈[-1,1],x2∈[1,+∞],求(m-2)2+(n-1)2的最小值.
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:(1)先求出函数的导数,得到故f′(x)=(x+1)(x-2),从而求出m,n的值,(2)由题意得不等式组,画出草图,将问题转化为求|AB|的长.
解答:
解:(1)由f(x)=
x3+
mx2+nx+2,
故f′x)=x2+mx+n,
函数f(x)有两个极值点-1和2,
故f′(x)=(x+1)(x-2),
∴m=-1,n=-2.
经检验,m=-1,n=-2满足题意.
(2)由函数f(x)有两个极值点x1和x2,且x1∈[-1,1],x2∈[1,+∞),
故有
,即
,
画出上述不等式组的可行域Ω如右图:
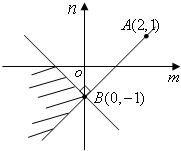
又(m-2)2+(n-1)2表示点(m,n)到点A(2,1)距离的平方.
而点A(2,1)到可行域Ω的点的最小距离是点A到点B(0,-1)的距离.
|AB|=
=2
∴(m-2)2+(n-1)2的最小值是|AB|2=(2
)2=8,
此时,m=0,n=-1;
经检验,m=0,n=-1满足题意.
| 1 |
| 3 |
| 1 |
| 2 |
故f′x)=x2+mx+n,
函数f(x)有两个极值点-1和2,
故f′(x)=(x+1)(x-2),
∴m=-1,n=-2.
经检验,m=-1,n=-2满足题意.
(2)由函数f(x)有两个极值点x1和x2,且x1∈[-1,1],x2∈[1,+∞),
故有
|
|
画出上述不等式组的可行域Ω如右图:

又(m-2)2+(n-1)2表示点(m,n)到点A(2,1)距离的平方.
而点A(2,1)到可行域Ω的点的最小距离是点A到点B(0,-1)的距离.
|AB|=
| (2-0)2+(1+1)2 |
| 2 |
∴(m-2)2+(n-1)2的最小值是|AB|2=(2
| 2 |
此时,m=0,n=-1;
经检验,m=0,n=-1满足题意.
点评:本题考察了利用导数研究函数的单调性问题,函数的最值问题,渗透了数形结合思想,是一道中档题.

练习册系列答案
相关题目
已知点P的极坐标为(2,
),那么过点P且平行于极轴的直线的极坐标方程是( )
| π |
| 4 |
A、ρsinθ=
| ||
| B、ρsinθ=2 | ||
C、ρcosθ=
| ||
| D、ρcosθ=2 |

