题目内容
已知直线AA′、BB′、CC′不共面，且AA′∥BB′，AA′=BB′，BB′∥CC′，BB′=CC′，求证：△ABC≌△A′B′C′．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由已知条件推导出四边形AA'B'B为平行四边形，四边形B'BCC'为平行四边形，由此能证明△ABC≌△A'B'C'．
解答：
解：∵AA′∥BB′，AA′=BB′，
∴四边形AA'B'B为平行四边形，
∵BB′∥CC′，BB′=CC′，
∴四边形B'BCC'为平行四边形
∴AB=A'B'，BC=B'C'，AA'∥CC'，且AA'=CC'，
∴四边形AA'C'C为平行四边形，∴AC=A'C'，
∴△ABC≌△A'B'C'．
∴四边形AA'B'B为平行四边形，
∵BB′∥CC′，BB′=CC′，
∴四边形B'BCC'为平行四边形
∴AB=A'B'，BC=B'C'，AA'∥CC'，且AA'=CC'，
∴四边形AA'C'C为平行四边形，∴AC=A'C'，
∴△ABC≌△A'B'C'．
点评：本题考查三角形全等的证明，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
在复平面内，O是原点，复数2+i与-3+4i（i为虚数单位）对应的向量分别是
与
，则向量
对应的复数是（ ）
| OA |
| OB |
| AB |
| A、-1+5i | B、-5+3i |
| C、5-3i | D、5-i |
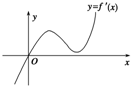定义在R上的函数f（x）满足f（4）=1，f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示．若两正数a，b满足f（2a+b）＜1，则