题目内容
已知等差数列{an}的公差d不等于0
(1)若数列{an}中的不同三项ar,as,at为等比数列,且r,s,t也为等比数列,证明:a1=d;
(2)若(a1)2+(a11)2=10,求a11+…+a21的最大值.
(1)若数列{an}中的不同三项ar,as,at为等比数列,且r,s,t也为等比数列,证明:a1=d;
(2)若(a1)2+(a11)2=10,求a11+…+a21的最大值.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)运用等差数列的通项公式和等比数列的性质,化简整理,得到2s(a1-d)=t(a1-d)+r(a1-d),注意运用公差d不等于0,即可得证;
(2)运用三角换元,令a1=
sinα,a11=
cosα,再由等差数列的求和公式,和辅助角公式,即可求出最大值.
(2)运用三角换元,令a1=
| 10 |
| 10 |
解答:
(1)证明:∵ar,as,at为等比数列,且r,s,t也为等比数列
∴as2=ar•at,s2=rt,
∴[a1+(s-1)d]2=[a1+(r-1)d]•[a1+(t-1)d]
∴2s(a1-d)=t(a1-d)+r(a1-d),
∵2s≠t+r,(否则s,r,t相等),
∴a1-d=0即a1=d;
(2)解:∵(a1)2+(a11)2=10,
∴令a1=
sinα,a11=
cosα,
∴10d=
(cosα-sinα),
∴a11+…+a21=
(a11+a21)•11=
[2
cosα+
(cosα-sinα)]•11
=
(3cosα-sinα)=
×10sin(α-θ)(θ为辅助角)≤55,
当且仅当sin(α+θ)=1,取最大值55.
∴as2=ar•at,s2=rt,
∴[a1+(s-1)d]2=[a1+(r-1)d]•[a1+(t-1)d]
∴2s(a1-d)=t(a1-d)+r(a1-d),
∵2s≠t+r,(否则s,r,t相等),
∴a1-d=0即a1=d;
(2)解:∵(a1)2+(a11)2=10,
∴令a1=
| 10 |
| 10 |
∴10d=
| 10 |
∴a11+…+a21=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 10 |
=
11
| ||
| 2 |
| 11 |
| 2 |
当且仅当sin(α+θ)=1,取最大值55.
点评:本题主要考查等差数列的通项和等比数列的性质及应用,考查三角换元法求最值,注意辅助角公式的运用,该题是一道综合题.

练习册系列答案
相关题目
已知平面向量
=(2,1),且
∥
,则
可能是( )
| a |
| a |
| b |
| b |
| A、(1,-2) |
| B、(-4,-2) |
| C、(-1,-2) |
| D、(4,-2) |
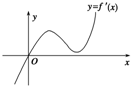 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E为棱AB的中点,求证:平面PCE⊥平面PCD.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E为棱AB的中点,求证:平面PCE⊥平面PCD.