题目内容
若ax2-（a-6）x+2＜0无解，求a的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：由题意可得a≥0，利用二次函数的性质分类讨论，求得a的范围．
解答：
解：∵ax2-（a-6）x+2＜0无解，∴a≥0．
当a=0时，不等式即6x+2＜0，解得 x＜-
，不满足条件．
当a＞0时，由△=（6-a）2-8a≤0，求得 2≤a≤18，
故a的取值范围为[2，18]．
当a=0时，不等式即6x+2＜0，解得 x＜-
| 1 |
| 3 |
当a＞0时，由△=（6-a）2-8a≤0，求得 2≤a≤18，
故a的取值范围为[2，18]．
点评：本题主要考查二次函数的性质的应用，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
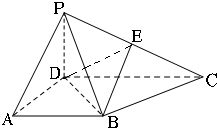如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AB∥CD，AD⊥CD，且AB=AD=PD=1，CD=2，E为PC的中点．