题目内容
设函数f(x)=ex-ax-2.
(Ⅰ)求函数f(x)=ex-ax-2的图象在点A(0,-1)处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
(Ⅰ)求函数f(x)=ex-ax-2的图象在点A(0,-1)处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)根据k=f′(0),再根据点斜式求出切线方程.
(Ⅱ)利用导数求函数的单调性;
(Ⅲ)求参数的取值范围,就求k的最值问题,利用导数求函数的最值,故当x>0时,(x-k)f/(x)+x+1>0?k<
+x(x>0).令g(x)=
+x,问题转化为求g(x)的最值问题.
(Ⅱ)利用导数求函数的单调性;
(Ⅲ)求参数的取值范围,就求k的最值问题,利用导数求函数的最值,故当x>0时,(x-k)f/(x)+x+1>0?k<
| x+1 |
| ex-1 |
| x+1 |
| ex-1 |
解答:
解:(Ⅰ)f(x)=ex-ax-2,x∈R,f′(x)=ex-a,x∈R,f′(0)=1-a,
函数f(x)=ex-ax-2的图象在点A(0,-1)处的切线方程为y=(1-a)x-1.
(Ⅱ)f′(x)=ex-a,x∈R.
若a≤0,则f′(x)>0恒成立,所以,f(x)在区间(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,lna)时,f′(x)<0,当x∈(lna,+∞)时,f′(x)>0,
所以,f(x)在区间(-∞,lna)上单调递减,在(lna,+∞)上单调递增.
( III)由于a=1,所以,(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.
故当x>0时,(x-k)f/(x)+x+1>0?k<
+x(x>0).①
令g(x)=
+x,则g/(x)=
+1=
.
函数h(x)=ex-x-2在(0,+∞)上单调递增,而h(1)<0,h(2)>0.
所以h(x)在(0,+∞)上存在唯一的零点,故g′(x)在(0,+∞)上存在唯一的零点.
设此零点为α,则α∈(1,2).当x∈(0,α)时,g′(x)<0;当x∈(α,+∞)时,g′(x)>0;
所以,g(x)在(0,+∞)上的最小值为g(α).由g′(α)=0,可得eα=α+2,
所以,g(α)=α+1∈(2,3).由于①式等价于k<g(α).
故整数k的最大值为2.
函数f(x)=ex-ax-2的图象在点A(0,-1)处的切线方程为y=(1-a)x-1.
(Ⅱ)f′(x)=ex-a,x∈R.
若a≤0,则f′(x)>0恒成立,所以,f(x)在区间(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,lna)时,f′(x)<0,当x∈(lna,+∞)时,f′(x)>0,
所以,f(x)在区间(-∞,lna)上单调递减,在(lna,+∞)上单调递增.
( III)由于a=1,所以,(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.
故当x>0时,(x-k)f/(x)+x+1>0?k<
| x+1 |
| ex-1 |
令g(x)=
| x+1 |
| ex-1 |
| -xex-1 |
| (ex-1)2 |
| ex(ex-x-2) |
| (ex-1)2 |
函数h(x)=ex-x-2在(0,+∞)上单调递增,而h(1)<0,h(2)>0.
所以h(x)在(0,+∞)上存在唯一的零点,故g′(x)在(0,+∞)上存在唯一的零点.
设此零点为α,则α∈(1,2).当x∈(0,α)时,g′(x)<0;当x∈(α,+∞)时,g′(x)>0;
所以,g(x)在(0,+∞)上的最小值为g(α).由g′(α)=0,可得eα=α+2,
所以,g(α)=α+1∈(2,3).由于①式等价于k<g(α).
故整数k的最大值为2.
点评:本题主要考查了导数和函数的单调性和最值的问题,求参数的取值范围经常就是转化为求某个函数的最值问题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
过点A(1,0)和点B(m,4)的直线与直线y=2x+1平行,则m等于( )
| A、3 | B、5 | C、7 | D、9 |
用数学归纳法证明12+32+52+…+(2n-1)2=
n(4n2-1)过程中,由n=k递推到n=k+1时,不等式左边增加的项为( )
| 1 |
| 3 |
| A、(2k)2 |
| B、(2k+3)2 |
| C、(2k+2)2 |
| D、(2k+1)2 |
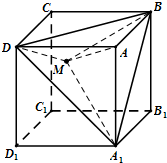 如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=(
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=( 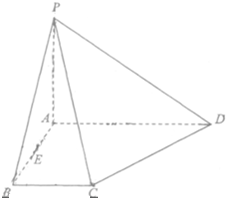 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点. 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为