题目内容
设等差数列{an}的前n项和为Sn,且S3=2S2+4,a5=36.
(Ⅰ)求an,Sn;
(Ⅱ)设bn=Sn-1(n∈N*),Tn=
+
+
+…+
,求Tn.
(Ⅰ)求an,Sn;
(Ⅱ)设bn=Sn-1(n∈N*),Tn=
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)依题意,布列首项a1与公差d的方程组,解之即可求得an,Sn;
(Ⅱ)bn=4n2-1=(2n-1)(2n+1)⇒
=
=
(
-
),于是可求得Tn=
+
+
+…+
.
(Ⅱ)bn=4n2-1=(2n-1)(2n+1)⇒
| 1 |
| bn |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
解答:
解:(Ⅰ)因为S3=2S2+4,
所以a1-d=-4,
又因为a5=36,
所以a1+4d=36…2分
解得d=8,a1=4,…3分
所以an=4+8(n-1)=8-4…4分
Sn=
=4n2…6分
(Ⅱ)bn=4n2-1=(2n-1)(2n+1)…7分
∴
=
=
(
-
)…9分
Tn=
+
+
+…+
=
(1-
+
-
+…+
-
)…10分
=
(1-
)=
…12分
所以a1-d=-4,
又因为a5=36,
所以a1+4d=36…2分
解得d=8,a1=4,…3分
所以an=4+8(n-1)=8-4…4分
Sn=
| n(4+8n-4) |
| 2 |
(Ⅱ)bn=4n2-1=(2n-1)(2n+1)…7分
∴
| 1 |
| bn |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
Tn=
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题考查数列的求和,着重考查等差数列的通项公式与求和公式的应用,突出列项法的考查,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为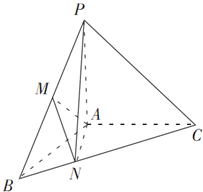 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=