题目内容
 已知正方体ABCD-A1B1C1D1,M为棱A1B1的中点,N为棱A1D1的中点.如图是该正方体被M,N,A所确定的平面和N,D,C1所确定的平面截去两个角后所得的几何体,则这个几何体的正视图为( )
已知正方体ABCD-A1B1C1D1,M为棱A1B1的中点,N为棱A1D1的中点.如图是该正方体被M,N,A所确定的平面和N,D,C1所确定的平面截去两个角后所得的几何体,则这个几何体的正视图为( )A、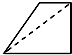 |
B、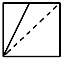 |
C、 |
D、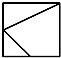 |
考点:简单空间图形的三视图
专题:规律型,空间位置关系与距离
分析:正视图是光线从几何体的前面向后面正投影得到的投影图,结合三视图的作法,即可判断出其正视图.
解答:
解:对于选项A,由于只是截去了两个角,此切割不可能使得正视图成为梯形.故A不对;
对于B,正视图是正方形符合题意,线段AM的影子是一个实线段,相对面上的线段DC1的投影是正方形的对角线,由于从正面看不到,故应作成虚线,故选项B正确;
对于C,正视图是正方形,符合题意,有两条实线存在于正面不符合实物图的结构,故不对;
对于D,正视图是正方形,符合题意,其中的两条实线符合俯视图的特征,故D不对.
故选:B
对于B,正视图是正方形符合题意,线段AM的影子是一个实线段,相对面上的线段DC1的投影是正方形的对角线,由于从正面看不到,故应作成虚线,故选项B正确;
对于C,正视图是正方形,符合题意,有两条实线存在于正面不符合实物图的结构,故不对;
对于D,正视图是正方形,符合题意,其中的两条实线符合俯视图的特征,故D不对.
故选:B
点评:本题考查三视图与几何体的关系,从正视图的定义可以判断出题中的正视图,同时要注意能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.

练习册系列答案
相关题目
曲线y=cosx(0≤x≤π)与y=-1围成的面积是( )
| A、0 | B、2 | C、4 | D、6 |
动点P满足
=
+λ[
+
],λ>0,则动点P的轨迹一定通过△ABC的( )
| OP |
| OA |
| ||
|
|
| ||
|
|
| A、重心 | B、垂心 | C、内心 | D、外心 |
如果函数f(x)=
-
(a>0)没有零点,则a的取值范围为( )
| a-x2 |
| 2 |
| A、(0,1) | ||
B、(
| ||
| C、(2,+∞) | ||
| D、(0,2) |
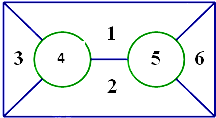 有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )
有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )| A、4320 | B、2880 |
| C、1440 | D、720 |
函数y=x32x的导函数是( )
| A、y′=3x22x |
| B、y′=2x32x |
| C、y′=3x22x+2xln2 |
| D、y′=3x22x+2xx3ln2 |
已知函数f(x)的导函数为f′(x),且满足f(x)=3f′(1)•x-x4,则f′(1)=( )
| A、-1 | B、-2 | C、1 | D、2 |
曲线f(x)=x2+3x在点A(1,4)处的切线斜率为( )
| A、2 | B、5 | C、6 | D、11 |
设{an}是递增的等差数列,a1+a2+a3=12,a1a2a3=48,则a1=( )
| A、1 | B、2 | C、4 | D、6 |