题目内容
已知函数f（x）的导函数为f′（x），且满足f（x）=3f′（1）•x-x4，则f′（1）=（ ）
| A、-1 | B、-2 | C、1 | D、2 |
考点：导数的运算
专题：导数的概念及应用
分析：求函数的导数，利用导数公式即可得到结论．
解答：
解：∵f（x）=3f′（1）•x-x4，
∴f′（x）=3f′（1）-4x3，
令x=1，则f′（1）=3f′（1）-4，
即f′（1）=2，
故选：D
∴f′（x）=3f′（1）-4x3，
令x=1，则f′（1）=3f′（1）-4，
即f′（1）=2，
故选：D
点评：本题主要考查导数的计算，要求熟练掌握常见函数的导数公式．
练习册系列答案
智能训练练测考系列答案
相关题目
在由l，2，3，4四个数字组成（允许重复）的四位数中，千位上的数字比个位上的数字小的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示的是由6个大小相同的正方体组成的几何体，它的俯视图是（ ）
A、 |
B、 |
C、 |
D、 |
已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为（ ）A、 |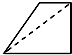
B、 |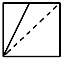
C、 |
D、 |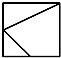
已知a＜b＜0，则下列不等式关系中不能成立的是（ ）
A、
| ||||
B、
| ||||
| C、|a|＞|b| | ||||
| D、a4＞b4 |
某咖啡厅为了了解热饮的销售量y（个）与气温x（℃）之间的关系，随机统计了某4天的销售量与气温，并制作了对照表：
由表中数据，得线性回归方程y=-2x+a．当气温为-4℃时，预测销售量约为（ ）
| 气温（℃） | 18 | 13 | 10 | -1 |
| 销售量（个） | 24 | 34 | 38 | 64 |
| A、68 | B、66 | C、72 | D、70 |
已知集合A={x|y=lgx}，B={x|y=
}，则A∩B=（ ）
| x2-2x |
| A、{x|x≥2} |
| B、{x|x＞2} |
| C、{x|x＞0} |
| D、{x|x≤0，或x≥2} |