题目内容
动点P满足
=
+λ[
+
]，λ＞0，则动点P的轨迹一定通过△ABC的（ ）
| OP |
| OA |
| ||
|
|
| ||
|
|
| A、重心 | B、垂心 | C、内心 | D、外心 |
考点：正弦定理,轨迹方程
专题：解三角形
分析：直接利用正弦定理以及平面向量基本定理化简已知表达式，通过向量的几何意义判断选项即可．
解答：
解：由正弦定理得：|
|sinB=|
|sinC，
所以
=
+λ[
+
]=
+
（
+
），
点P在BC边的中线上，即点P的轨迹过三角形的重心．
故选：A．
| AB |
| AC |
所以
| OP |
| OA |
| ||
|
|
| ||
|
|
| OA |
| λ | ||
|
|
| AB |
| AC |
点P在BC边的中线上，即点P的轨迹过三角形的重心．
故选：A．
点评：本题考查向量的基本运算以及正弦定理的应用，基本知识的考查．
练习册系列答案
相关题目
口袋里放有大小相同的两个红球和一个白球，有放回地每次摸取一个球，定义数列{an}，an=
，如果Sn为数列{an}的前n项和，那么S5=3的概率为（ ）
|
A、C
| ||||||
B、C
| ||||||
C、C
| ||||||
D、C
|
在由l，2，3，4四个数字组成（允许重复）的四位数中，千位上的数字比个位上的数字小的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知中心在坐标原点，焦点在x轴上的双曲线C的渐近线方程为y=±2x，则此双曲线的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、5 |
已知函数f（x+1）是偶函数，且x＞1时，f′（x）＜0恒成立，又f（4）=0，则（x+3）f（x+4）＜0的解集为（ ）
| A、（-∞，-2）∪（4，+∞） |
| B、（-6，-3）∪（0，4） |
| C、（-∞，-6）∪（4，+∞） |
| D、（-6，-3）∪（0，+∞） |
2010年11月1日开始，我国开始了第6次全国人口普查，据统计，育龄妇女生男生女是等可能的，如果某个家庭共有了两个孩子，有一个是女孩，则这时另一个孩子是男孩的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示的是由6个大小相同的正方体组成的几何体，它的俯视图是（ ）
A、 |
B、 |
C、 |
D、 |
已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为（ ）A、 |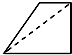
B、 |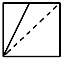
C、 |
D、 |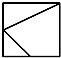
已知集合A={x|y=lgx}，B={x|y=
}，则A∩B=（ ）
| x2-2x |
| A、{x|x≥2} |
| B、{x|x＞2} |
| C、{x|x＞0} |
| D、{x|x≤0，或x≥2} |