题目内容
如果函数f（x）=
-
（a＞0）没有零点，则a的取值范围为（ ）
| a-x2 |
| 2 |
| A、（0，1） | ||
B、（
| ||
| C、（2，+∞） | ||
| D、（0，2） |
考点：函数零点的判定定理,函数的零点
专题：函数的性质及应用
分析：如果函数f（x）=
-
（a＞0）没有零点，则方程
=
（a＞0）没有实数根，进而可得答案．
| a-x2 |
| 2 |
| a-x2 |
| 2 |
解答：
解：若函数f（x）=
-
（a＞0）没有零点，
则方程
=
（a＞0）没有实数根，
即方程a-x2=2（a＞0）没有实数根，
即方程x2=a-2（a＞0）没有实数根，
故a-2＜0且a＞0，
故a的取值范围为（0，2），
故选：D
| a-x2 |
| 2 |
则方程
| a-x2 |
| 2 |
即方程a-x2=2（a＞0）没有实数根，
即方程x2=a-2（a＞0）没有实数根，
故a-2＜0且a＞0，
故a的取值范围为（0，2），
故选：D
点评：本题考查的知识点是函数零点的判定，函数的零点，其中将问题转化为方程
=
（a＞0）没有实数根，是解答的关键．
| a-x2 |
| 2 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
甲、乙两位同学，升入高三以来连续五次模拟考试数学单科成绩如表：
则平均成绩较高与成绩较稳定的分别是（ ）
| 甲 | 108 | 112 | 110 | 109 | 111 |
| 乙 | 109 | 111 | 108 | 108 | 109 |
| A、同学甲，同学甲 |
| B、同学甲，同学乙 |
| C、同学乙，同学甲 |
| D、同学乙，同学乙 |
已知中心在坐标原点，焦点在x轴上的双曲线C的渐近线方程为y=±2x，则此双曲线的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、5 |
2010年11月1日开始，我国开始了第6次全国人口普查，据统计，育龄妇女生男生女是等可能的，如果某个家庭共有了两个孩子，有一个是女孩，则这时另一个孩子是男孩的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示的是由6个大小相同的正方体组成的几何体，它的俯视图是（ ）
A、 |
B、 |
C、 |
D、 |
已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为（ ）A、 |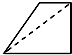
B、 |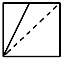
C、 |
D、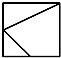 |