题目内容
设{an}是递增的等差数列，a1+a2+a3=12，a1a2a3=48，则a1=（ ）
| A、1 | B、2 | C、4 | D、6 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的性质求出a2的值，然后得到a1，a3的方程组，从而求出a1，a3的值．
解答：
解：由等差数列的性质可知，a1+a3=2a2，
所以a1+a2+a3=3a2=12，则a2=4，
所以得a1+a3=8，a1a3=12，
因为{an}是递增的等差数列，
所以解得a1=2，a3=6；
故选：B．
所以a1+a2+a3=3a2=12，则a2=4，
所以得a1+a3=8，a1a3=12，
因为{an}是递增的等差数列，
所以解得a1=2，a3=6；
故选：B．
点评：本题主要考查了等差数列的性质，以及通项公式，同时考查了运算求解的能力，属于基础试题．
练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为（ ）A、 |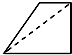
B、 |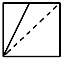
C、 |
D、 |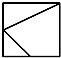
已知集合A={x|y=lgx}，B={x|y=
}，则A∩B=（ ）
| x2-2x |
| A、{x|x≥2} |
| B、{x|x＞2} |
| C、{x|x＞0} |
| D、{x|x≤0，或x≥2} |
给出下列四个命题：
①因为（4+3i）-（2+3i）=2＞0，所以4+3i＞2+3i；
②由
•
=
•
两边同除
，可得
=
；
③数列1，4，7，10，…，3n+7的一个通项公式是an=3n+7；
④演绎推理是由一般到特殊的推理，类比推理是由特殊到特殊的推理．
其中正确命题的个数有（ ）
①因为（4+3i）-（2+3i）=2＞0，所以4+3i＞2+3i；
②由
| a |
| b |
| a |
| c |
| a |
| b |
| c |
③数列1，4，7，10，…，3n+7的一个通项公式是an=3n+7；
④演绎推理是由一般到特殊的推理，类比推理是由特殊到特殊的推理．
其中正确命题的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知数列an：
，
，
，
，
，
，
，
，
，
，…，依它的前10项的规律，则a99+a100的值为（ ）
| 1 |
| 1 |
| 2 |
| 1 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|