题目内容
设集合A={-4，0}，B={x|（x+a）（x+4）=0}，若A∪B=B，求实数a构成的集合．
考点：并集及其运算
专题：集合
分析：求出B中方程的解确定出B，根据A与B并集为B，求出a的值，即可确定出实数a构成的集合．
解答：
解：由B中的方程得：x+a=0或x+4=0，
即x=-a或x=-4，
∴B={-a，-4}，
∵A={-4，0}，A∪B=B，
即A⊆B，
∴a=0，
则实数a构成的集合为{0}．
即x=-a或x=-4，
∴B={-a，-4}，
∵A={-4，0}，A∪B=B，
即A⊆B，
∴a=0，
则实数a构成的集合为{0}．
点评：此题考查了并集及其运算，熟练掌握并集的定义是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
命题p：对任意的实数m，使方程x2+mx+1=0无实数根，则“￢p”形式的命题是（ ）
| A、不存在实数m，使方程x2+mx+1=0有实根 |
| B、存在实数m，使方程x2+mx+1=0有实根 |
| C、有一些的实数m，使得方程x2+mx+1=0无实根 |
| D、至多有一个实根m，使得方程x2+mx+1=0有实根 |
-60°角是第（ ）象限角．
| A、一 | B、二 | C、三 | D、四 |
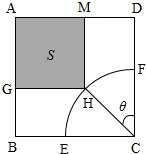如图，体育馆计划用运动场的边角地建造一个矩形健身室，四边形ABCD是一块正方形地皮，边长为a（a＞40m），扇形CEF是运动场的一部分，半径为40m，矩形AGHM就是计划的健身室，其中G、M分别在AB、AD上，H在