题目内容
已知数列{an}中，a1=1，a2=4，且各项均满足an+2=an+1+2an，求数列{an}的通项公式．
考点：数列递推式
专题：计算题,等差数列与等比数列
分析：由an+2=an+1+2an，两边同加an+1，得an+2+an+1=2（an+1+an），可判断{an+1+an}是等比数列，从而可得an+1+an=5•2n-1①；由an+2=an+1+2an，两边同减2an+1，得an+2-2an+1=-（an+1-2an），可判断{an+1-2an}是等比数列，从而可得an+1-2an=2•（-1）n-1②，联立①②可得结果．
解答：
解：an+2=an+1+2an，两边同加an+1，得an+2+an+1=2（an+1+an），
又a1=1，a2=4，∴{an+1+an}是首项为5，公比为2的等比数列，
∴an+1+an=5•2n-1①；
an+2=an+1+2an，两边同减2an+1，得an+2-2an+1=-（an+1-2an），
∴{an+1-2an}是首项为2，公比为-1的等比数列，
∴an+1-2an=2•（-1）n-1②，
由①②得an=
•2n-1-
•(-1)n-1．
又a1=1，a2=4，∴{an+1+an}是首项为5，公比为2的等比数列，
∴an+1+an=5•2n-1①；
an+2=an+1+2an，两边同减2an+1，得an+2-2an+1=-（an+1-2an），
∴{an+1-2an}是首项为2，公比为-1的等比数列，
∴an+1-2an=2•（-1）n-1②，
由①②得an=
| 5 |
| 3 |
| 2 |
| 3 |
点评：本题考查由数列递推式求数列通项、等比数列的定义及通项公式，考查学生推理论证能力、分析问题解决问题的能力．
练习册系列答案
名校课堂系列答案
相关题目
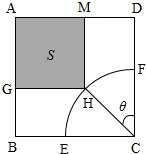如图，体育馆计划用运动场的边角地建造一个矩形健身室，四边形ABCD是一块正方形地皮，边长为a（a＞40m），扇形CEF是运动场的一部分，半径为40m，矩形AGHM就是计划的健身室，其中G、M分别在AB、AD上，H在
