题目内容
设函数f（x）=log2（3x-1），若f（x）＞2，求x的取值范围．
考点：对数函数的图像与性质
专题：不等式的解法及应用
分析：根据对数函数和指数函数的性质，即可解不等式．
解答：
解：∵f（x）=log2（3x-1），
∴由f（x）＞2，
得f（x）=log2（3x-1）＞2，
即3x-1＞4，
∴3x＞5，
即x＞log35，
∴x的取值范围是x＞log35．
∴由f（x）＞2，
得f（x）=log2（3x-1）＞2，
即3x-1＞4，
∴3x＞5，
即x＞log35，
∴x的取值范围是x＞log35．
点评：本题主要考查不等式的解法，利用对数函数和指数函数的性质是解决本题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
设集合I={1，2，3，4}．选择集合I的两个非空子集A和B，要使集合B中最小的数大于集合A中最大的数，则不同的选择方法共有（ ）
| A、16种 | B、17种 |
| C、18种 | D、19种 |
已知数列{an}，{bn}（n∈N*）都是公差为1的等差数列，其首项分别为a1，b1，且a1+b1=5，则数列{an+bn}的前10项的和等于（ ）
| A、85 | B、95 |
| C、120 | D、140 |
函数y=x2-6x+5在区间（0，5）上是（ ）
| A、递增函数 |
| B、递减函数 |
| C、先递减后递增 |
| D、先递增后递减 |
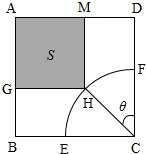如图，体育馆计划用运动场的边角地建造一个矩形健身室，四边形ABCD是一块正方形地皮，边长为a（a＞40m），扇形CEF是运动场的一部分，半径为40m，矩形AGHM就是计划的健身室，其中G、M分别在AB、AD上，H在