题目内容
如图阴影部分可用二元一次不等式组表示为 .


考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:分别求出每条直线对应的方程,根据二元二次不等式组表示平面区域,即可得到结论.
解答:
解:由图象可知,过点(-2,0)和(0,4)的直线方程为
+
=1,
即y=2x+4,
则不等式组对应的平面区域为
,
故答案为:
.
| x |
| -2 |
| y |
| 4 |
即y=2x+4,
则不等式组对应的平面区域为
|
故答案为:
|
点评:本题主要考查二元二次不等式组表示平面区域,确定直线方程是解决本题的关键,比较基础.

练习册系列答案
相关题目
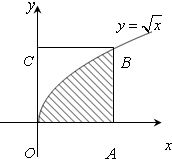 在边长为1的正方形OABC中任取一点P,则点P恰好落在正方形与曲线y=
在边长为1的正方形OABC中任取一点P,则点P恰好落在正方形与曲线y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知非负实数a,b满足a+b≤1,则关于x的一元二次方程x2+ax+b2=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是某城市的一个艺术雕塑几何体的三视图,根据图中数据,可得该几何体的表面积是( )


| A、264 | B、228 |
| C、192 | D、156 |
设函数f(x)=x2+
-a(x≠0),a为常数且a>2,则f(x)的零点个数是( )
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
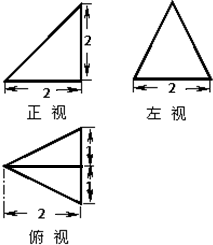 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
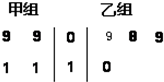 如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.
如图茎叶图记录了甲、乙两组各四名同学的植树的棵数. 如图阴影部分可用不等式表示为
如图阴影部分可用不等式表示为