题目内容
设集合Ω为平面内的点集,对于给定的点A,若存在点P0∈Ω,使得对任意的点P∈Ω,均有|AP|≥|AP0|,则定义|AP0|为点A到点集Ω的距离.已知点集Ω={(x,y)|
},则平面内到Ω的距离为1的动点A的轨迹所围成图形的面积为 .
|
考点:轨迹方程
专题:不等式的解法及应用
分析:确定点集Ω={(x,y)|
}表示的平面区域,可得平面内到Ω的距离为1的动点A的轨迹所围成图形的面积为半径为1的圆的面积加上三个矩形的面积加上直角三角形的面积,即可得出结论.
|
解答:
 解:点集Ω={(x,y)|
解:点集Ω={(x,y)|
}表示的平面区域如图所示.
三角形三个顶点的坐标为(1,1),(3,3),(3,-1),则直角三角形的三边边长为4,2
,2
,
∴平面内到Ω的距离为1的动点A的轨迹所围成图形的面积为半径为1的圆的面积加上三个矩形的面积加上直角三角形的面积,
∴S=π+2
+2
+4+
•2
•2
=8+4
+π.
故答案为:8+4
+π.
 解:点集Ω={(x,y)|
解:点集Ω={(x,y)|
|
三角形三个顶点的坐标为(1,1),(3,3),(3,-1),则直角三角形的三边边长为4,2
| 2 |
| 2 |
∴平面内到Ω的距离为1的动点A的轨迹所围成图形的面积为半径为1的圆的面积加上三个矩形的面积加上直角三角形的面积,
∴S=π+2
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:8+4
| 2 |
点评:本题考查新定义,考查不打折表示的平面区域,考查图形面积的计算,考查学生分析解决问题的能力,确定图形的形状是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=(ax+1)(x-a)为偶函数,且函数y=f(x)在x∈(0,+∞)上单调递增,则实数a的值为( )
| A、±1 | B、-1 | C、1 | D、0 |
下列函数中,最小正周期为π的偶函数为( )
A、y=sin(x+
| ||||
B、y=
| ||||
| C、y=2tan2x | ||||
| D、y=sinxcosx |
某几何体的三视图如图所示,则这个几何体的直视图是图中的( )


A、 |
B、 |
C、 |
D、 |
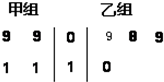 如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.
如图茎叶图记录了甲、乙两组各四名同学的植树的棵数. 如图阴影部分可用不等式表示为
如图阴影部分可用不等式表示为