题目内容
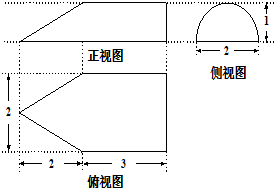
某几何体的三视图(如图),则该几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图知几何体是左边为一半圆锥,右边为半圆柱的组合体,根据三视图的数据判断圆锥与圆柱的底面圆直径为2,圆柱的高为3,圆锥的高为2,利用体积公式计算可得答案.
解答:
解:由三视图知几何体是左边为一半圆锥,右边为半圆柱的组合体,
且圆锥与圆柱的底面圆直径为2,圆柱的高为3,圆锥的高为2,
∴几何体的体积V=V半圆柱+V半圆锥=
π×12×3+
×
×π×12×2=
π.
故选B.
且圆锥与圆柱的底面圆直径为2,圆柱的高为3,圆锥的高为2,
∴几何体的体积V=V半圆柱+V半圆锥=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 11 |
| 6 |
故选B.
点评:本题考查了由三视图求几何体的体积,解题的关键是判断几何体的形状及相关数据所对应的几何量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
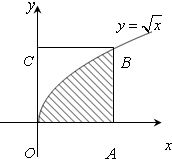 在边长为1的正方形OABC中任取一点P,则点P恰好落在正方形与曲线y=
在边长为1的正方形OABC中任取一点P,则点P恰好落在正方形与曲线y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=(ax+1)(x-a)为偶函数,且函数y=f(x)在x∈(0,+∞)上单调递增,则实数a的值为( )
| A、±1 | B、-1 | C、1 | D、0 |
已知非负实数a,b满足a+b≤1,则关于x的一元二次方程x2+ax+b2=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=x2+
-a(x≠0),a为常数且a>2,则f(x)的零点个数是( )
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
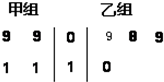 如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.
如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.