题目内容
已知f(α)=
(1)化简f(a);
(2)若cosα+2sinα=-
,求f(a)的值.
sin(π-α)cos(2π-α)sin(-α+
| ||
cos(-π-α)cos(-α+
|
(1)化简f(a);
(2)若cosα+2sinα=-
| 5 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:(1)根据三角函数的诱导公式进行化简即可得到f(a);
(2)利用三角函数的关系利用cosα+2sinα=-
,即可求f(a)的值.
(2)利用三角函数的关系利用cosα+2sinα=-
| 5 |
解答:
解:(1)f(α)=
=
=sinα•
=-cosα,
(2)∵cosα+2sinα=-
,
∴联立方程sin2α+cos2α=1,
解得cosα=-
,
∴f(α)=-cosα=
.
sin(π-α)cos(2π-α)sin(-α+
| ||
cos(-π-α)cos(-α+
|
sinα•cosα•sin(α-
| ||
cosα•cos(α-
|
| -cosα |
| sinα |
(2)∵cosα+2sinα=-
| 5 |
∴联立方程sin2α+cos2α=1,
解得cosα=-
| ||
| 5 |
∴f(α)=-cosα=
| ||
| 5 |
点评:本题主要考查三角函数的诱导公式的应用,要求熟练掌握三角函数的公式,考查学生的计算能力.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
已知非负实数a,b满足a+b≤1,则关于x的一元二次方程x2+ax+b2=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是某城市的一个艺术雕塑几何体的三视图,根据图中数据,可得该几何体的表面积是( )


| A、264 | B、228 |
| C、192 | D、156 |
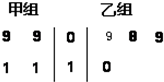 如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.
如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.