题目内容
若一次函数y=kx+b在(-∞,+∞)上是减函数,则点(k,b)在直角坐标平面的( )
| A、上半平面 | B、下半平面 |
| C、左半平面 | D、右半平面 |
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:根据一次函数的单调性求出k的符号,然后根据斜率的符号,确定点的位置.
解答:
解:∵一次函数y=kx+b在(-∞,+∞)上是减函数,
∴k<0,
则点(k,b)在直角坐标平面的位于平面坐标系中的左半平面,
故选:C.
∴k<0,
则点(k,b)在直角坐标平面的位于平面坐标系中的左半平面,
故选:C.
点评:本题主要考查一次函数的单调性的性质,以及点在平面坐标系的位置,比较基础.

练习册系列答案
相关题目
设函数f(x)=x2+
-a(x≠0),a为常数且a>2,则f(x)的零点个数是( )
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
某几何体的三视图如图所示,则这个几何体的直视图是图中的( )


A、 |
B、 |
C、 |
D、 |
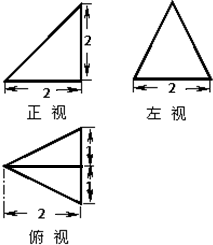 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
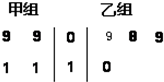 如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.
如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.