题目内容
数列{an}各项均不为0,前n项和为Sn,bn=an3,bn的前n项和为Tn,且Tn=Sn2
(1)若数列{an}共3项,求所有满足要求的数列;
(2)求证:an=n(n∈N*)是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列{an},并使得a2015=-2014;若还能构造其他符合要求的数列,请一并写出(不超过四个).
(1)若数列{an}共3项,求所有满足要求的数列;
(2)求证:an=n(n∈N*)是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列{an},并使得a2015=-2014;若还能构造其他符合要求的数列,请一并写出(不超过四个).
考点:数学归纳法,数列的求和
专题:压轴题,点列、递归数列与数学归纳法
分析:(1)依题意,分n=1、2、3,三类讨论,可得所有满足要求的数列;
(2)利用数学归纳法证明即可;
(3)由Sn2=a13+a23+…+an3①,Sn+12=a13+a23+…+an3+an+13②,联立①②,可整理得到:(an+1+an)(an+1-an-1)=0,于是,可求得一个满足已知条件的无穷数列{an},并使得a2015=-2014;再购造其他符合要求的数列四个即可.
(2)利用数学归纳法证明即可;
(3)由Sn2=a13+a23+…+an3①,Sn+12=a13+a23+…+an3+an+13②,联立①②,可整理得到:(an+1+an)(an+1-an-1)=0,于是,可求得一个满足已知条件的无穷数列{an},并使得a2015=-2014;再购造其他符合要求的数列四个即可.
解答:
(本题(18分),第一小题(4分),第二小题(6分),第三小题8分)
解:(1)n=1时,T1=S12⇒a13=a12⇒a1=1(a1=0舍去)…(1分)
n=2时,T2=S22⇒a13+a23=(a1+a2)2⇒1+a23=(1+a2)2⇒a2=2或a2=-1(a2=0舍去)…(2分)
n=3时,T3=
⇒
+
+
=(a1+a2+a3)2,
当a2=2时,1+8+
=(1+2+a3)2⇒a3=3或a3=-2(a3=0舍去)
当a2=-1时,1-1+
=(1-1+a3)2⇒a3=1(a3=0舍去)…(3分)
所以符合要求的数列有:1,2,3;1,2,-2;1,-1,1…(4分)
(2)∵an=n,即证13+23+33+…+n3=(1+2+3+…+n)2,…(5分)
用数学归纳法证:
当n=1时,13=12,等式成立;
假设当n=k时,13+23+33+…+k3=(1+2+3+…+k)2=[
]2,…(7分)
则当n=k+1时,13+23+33+…+k3+(k+1)3=(1+2+3+…+k)2+(k+1)3
=[
]2+(k+1)3=(
)2(k2+4k+4)
=[
]2=[
]2,即当n=k+1时,等式也成立;
综上所述,对任意n∈N*,13+23+33+…+n3=(1+2+3+…+n)2;…(10分)
(3)Sn2=a13+a23+…+an3①
Sn+12=a13+a23+…+an3+an+13②
②-①得:2Sn+an+1=an+12,
∴2Sn=an+12-an+1;③…(11分)
∴当n≥2时,2Sn-1=an2-an,④…(12分)
③-④得:2an=an+12-an+1-an2+an,
整理得:(an+1+an)(an+1-an-1)=0,
∴an+1=-an,或an+1=an+1(n≥2)…(14分)
(i)an=
;
(ii)an=
;
(iii)an=
;
(v)an=
解:(1)n=1时,T1=S12⇒a13=a12⇒a1=1(a1=0舍去)…(1分)
n=2时,T2=S22⇒a13+a23=(a1+a2)2⇒1+a23=(1+a2)2⇒a2=2或a2=-1(a2=0舍去)…(2分)
n=3时,T3=
| S | 2 3 |
| a | 3 1 |
| a | 3 2 |
| a | 3 3 |
当a2=2时,1+8+
| a | 3 3 |
当a2=-1时,1-1+
| a | 3 3 |
所以符合要求的数列有:1,2,3;1,2,-2;1,-1,1…(4分)
(2)∵an=n,即证13+23+33+…+n3=(1+2+3+…+n)2,…(5分)
用数学归纳法证:
当n=1时,13=12,等式成立;
假设当n=k时,13+23+33+…+k3=(1+2+3+…+k)2=[
| k(k+1) |
| 2 |
则当n=k+1时,13+23+33+…+k3+(k+1)3=(1+2+3+…+k)2+(k+1)3
=[
| k(k+1) |
| 2 |
| k+1 |
| 2 |
=[
| (k+1)(k+2) |
| 2 |
| (k+1)((k+1)+1) |
| 2 |
综上所述,对任意n∈N*,13+23+33+…+n3=(1+2+3+…+n)2;…(10分)
(3)Sn2=a13+a23+…+an3①
Sn+12=a13+a23+…+an3+an+13②
②-①得:2Sn+an+1=an+12,
∴2Sn=an+12-an+1;③…(11分)
∴当n≥2时,2Sn-1=an2-an,④…(12分)
③-④得:2an=an+12-an+1-an2+an,
整理得:(an+1+an)(an+1-an-1)=0,
∴an+1=-an,或an+1=an+1(n≥2)…(14分)
(i)an=
|
(ii)an=
|
(iii)an=
|
(v)an=
|
点评:本题考查数列的求和,考查数学归纳法的应用,突出考查构造函数数学、化归思想及创新思维、逻辑思维、综合运算能力,属于难题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知x,y为正实数,则( )
| A、10lnx-lny=10lnx-10lny | ||||
B、10ln(x-y)=
| ||||
C、10
| ||||
D、10 ln
|
设x=
,y=3-
,集合M={m|m=a+b
,a∈Q,b∈Q},那么x,y与集合M的关系是( )
| 1 | ||
3+2
|
| 2 |
| 2 |
| A、x∈M,y∈M |
| B、x∈M,y∉M |
| C、x∉M,y∈M |
| D、x∉M,y∉M |
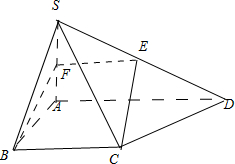 在四棱锥S-ABCD中,底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA=
在四棱锥S-ABCD中,底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA=