题目内容
已知函数f(x)=
的定义域为集合A,不等式
≥1的解集为B.
(1)求(∁RA)∩B
(2)记A∪B=C,若集合M={x∈R||x-a|<4}满足M∩C=ϕ,求实数a的取值范围.
| 1 |
| log2(3x-2) |
| 1 |
| 2-x |
(1)求(∁RA)∩B
(2)记A∪B=C,若集合M={x∈R||x-a|<4}满足M∩C=ϕ,求实数a的取值范围.
考点:交、并、补集的混合运算
专题:集合
分析:先根据解析式求出函数的定义域A,由分式不等式的解法求出
≥1的解集B,
(1)由补集的运算求出CRA,再由交集的运算求出(CRA)∩B;
(2)由并集的运算求出集合C,求出绝对值不等式|x-a|<4的解集即可求出M,再由M∩C=ϕ列出不等式,求实数a的取值范围.
| 1 |
| 2-x |
(1)由补集的运算求出CRA,再由交集的运算求出(CRA)∩B;
(2)由并集的运算求出集合C,求出绝对值不等式|x-a|<4的解集即可求出M,再由M∩C=ϕ列出不等式,求实数a的取值范围.
解答:
解:由
得,解得x>
且x≠1,即A={x|x>
且x≠1},
由
≥1得,
≤0,即
,
解得1≤x<2,则B={x|1≤x<2}. …(4分)
(1)于是CRA={x|x≤
或x=1},所以(CRA)∩B={1}.…(6分)
(2)因为A∪B={x|x>
},则C={x|x>
},
由|x-a|<4得,a-4<x<a+4,即M={x|a-4<x<a+4},
因为M∩C=∅,所以a+4≤
,解得a≤-
.…(12分)
|
| 2 |
| 3 |
| 2 |
| 3 |
由
| 1 |
| 2-x |
| x-1 |
| x-2 |
|
解得1≤x<2,则B={x|1≤x<2}. …(4分)
(1)于是CRA={x|x≤
| 2 |
| 3 |
(2)因为A∪B={x|x>
| 2 |
| 3 |
| 2 |
| 3 |
由|x-a|<4得,a-4<x<a+4,即M={x|a-4<x<a+4},
因为M∩C=∅,所以a+4≤
| 2 |
| 3 |
| 10 |
| 3 |
点评:本题考查了交、并、补集的混合运算,分式不等式、绝对值的解法,以及函数的定义域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等差数列{an}中,a5=10,则a3+a7等于( )
| A、10 | B、15 | C、20 | D、25 |
双曲线
+
=1的焦距为( )
| x2 |
| a |
| y2 |
| a-1 |
| A、1 | ||
| B、2 | ||
C、2
| ||
D、2
|
数列{an}中,若an+1=
,a1=1,则a2010=( )
| an |
| 2an+1 |
| A、4019 | ||
B、
| ||
| C、4021 | ||
D、
|
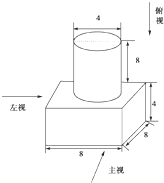 一几何体的直观图如图所示:
一几何体的直观图如图所示: