题目内容
先后抛掷两颗均匀的骰子,问:
(1)至少有一颗是5点的概率是多少?
(2)当第一颗骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.
(1)至少有一颗是5点的概率是多少?
(2)当第一颗骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.
考点:古典概型及其概率计算公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)从中找出至少有一个骰子的点数为5的个数,再用古典概型计算公式,即可得到所求的概率;
(2)从中找出第一颗骰子的点数为3或6时的个数,再找出其中两颗骰子的点数之和大于8的个数,再用古典概型计算公式,即可得到所求的概率;
(2)从中找出第一颗骰子的点数为3或6时的个数,再找出其中两颗骰子的点数之和大于8的个数,再用古典概型计算公式,即可得到所求的概率;
解答:
(1)同时投掷两个骰子,可能出现的结果有如下36种:
满足至少有一个骰子的点数是5的结果有11种,所求概率为P=
,
(2)第一颗骰子的点数为3或6有12种结果,
其中两颗骰子的点数之和大于8的有(3,6),(6,3),(6,4),(6,5),(6,6)共5个,
∴两颗骰子的点数之和大于8的概率是
.
满足至少有一个骰子的点数是5的结果有11种,所求概率为P=
| 11 |
| 36 |
(2)第一颗骰子的点数为3或6有12种结果,
其中两颗骰子的点数之和大于8的有(3,6),(6,3),(6,4),(6,5),(6,6)共5个,
∴两颗骰子的点数之和大于8的概率是
| 5 |
| 12 |
点评:本题考查了古典概型的概率计算,解题的关键是求得符合条件的基本事件个数.

练习册系列答案
相关题目
已知空间四边形ABCD,E,F,G,H分别边AB,BC,CD,DA的中点,则EG与FH位置关系是( )
| A、相交 | B、平行 | C、异面 | D、重合 |
双曲线
-
=1的离心率e∈(1,2),则实数k的取值范围是( )
| x2 |
| 4 |
| y2 |
| k |
| A、(0,4) | ||
| B、(1,1) | ||
C、(0,2
| ||
| D、(0,12) |
在正方体ABCD-A1B1C1D1中,下列各 式运算结果为向量
的是( )
①(
-
)-
;
②(
+
)-
;
③(
-
)-
;
④(
-
)+
.
| BD1 |
①(
| A1D1 |
| A1A |
| AB |
②(
| BC |
| BB1 |
| D1C1 |
③(
| AD |
| AB |
| DD1 |
④(
| B1D1 |
| A1A |
| DD1 |
| A、①② | B、②③ | C、③④ | D、①④ |
函数f(x)=1-log3x的零点是( )
| A、(1,1) | B、1 |
| C、(3,0) | D、3 |
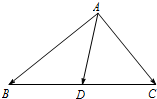 如图,点D是线段BC的中点,BC=6,且|
如图,点D是线段BC的中点,BC=6,且|| AB |
| AC |
| AB |
| AC |
| AD |
| A、6 | ||
B、2
| ||
| C、3 | ||
D、
|
 已知函数f(x)=
已知函数f(x)=