题目内容
设{an}是等差数列，Sn是其前n项和，若S2≤3，S3≥6，则S4的最小值为 ．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：设等差数列{an}的公差为d，由题意可得可得2a1+d≤3，a1+d≥2，而S4=4a1+6d=-2（2a1+d）+8（a1+d），由不等式的性质可得范围．
解答：
解：设等差数列{an}的公差为d，
则S2=2a1+d≤3，S3=3a1+3d≥6，
整理可得2a1+d≤3，a1+d≥2，
设S4=4a1+6d=x（2a1+d）+y（a1+d）=（2x+y）a1+（x+y）d，
则
，解得
，
∴S4=4a1+6d=-2（2a1+d）+8（a1+d）≥10
故答案为：10
则S2=2a1+d≤3，S3=3a1+3d≥6，
整理可得2a1+d≤3，a1+d≥2，
设S4=4a1+6d=x（2a1+d）+y（a1+d）=（2x+y）a1+（x+y）d，
则
|
|
∴S4=4a1+6d=-2（2a1+d）+8（a1+d）≥10
故答案为：10
点评：本题考查等差数列的求和公式，涉及不等式的性质和整体思想，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知{an}为等比数列，Sn是它的前n项和．若a2•a3=2a1，且a4与2a7的等差中项为
，则S5=（ ）
| 5 |
| 4 |
| A、31 | B、32 | C、33 | D、34 |
函数y=sin（
-2x）cos（
+2x）的周期及单调递减区间分别是（ ）
| π |
| 6 |
| π |
| 6 |
A、
| ||||||||||
B、π（
| ||||||||||
C、
| ||||||||||
D、
|
如图，在同一直角坐标系中，正确表示直线y=ax与y=x+a的是（ ）
A、 |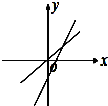
B、 |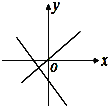
C、 |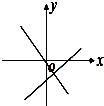
D、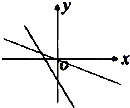 |