题目内容
已知f（x）是以2为周期的奇函数，在区间[0，1]上的解析式为f（x）=2x，则f（11.5）= ．
考点：函数的周期性
专题：计算题,函数的性质及应用
分析：由f（x）是以2为周期的奇函数知f（11.5）=-f（0.5）=-1．
解答：
解：∵f（x）是以2为周期的奇函数，
∴f（11.5）=f（12-0.5）
=f（-0.5）=-f（0.5）=-1；
故答案为：-1．
∴f（11.5）=f（12-0.5）
=f（-0.5）=-f（0.5）=-1；
故答案为：-1．
点评：本题考查了函数的性质的应用，属于基础题．
练习册系列答案
相关题目
解决某一问题而设计的 （ ） 有限的步骤称为算法．
| A、确定的 | B、有效的 |
| C、连续的 | D、无穷的 |
已知m，n是两条不重合的直线，α，β，γ是三个两两不重合的平面，给出下列四个命题
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
| A、①和② | B、①和③ |
| C、①和④ | D、③和④ |
已知{an}是等差数列，若a2+a4=6，a5=5，数列{bn}满足bn=anan+1，则
+
+…+
等于（ ）
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
A、
| ||
B、
| ||
C、
| ||
D、
|
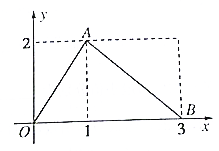函数y=f（x）的图象是如图所示的折线段OAB，已知点A坐标为（1，2）点B的坐标为（3，0），若P（x，y）是函数g（x）=f（x）（x-1）图象上的动点，则x+y的最大值为（ ）