题目内容

函数y=sin（
π
6
-2x）cos（
π
6
+2x）的周期及单调递减区间分别是（　　）
A、
π
2
，（
kπ
2
+
π
8
，
kπ
2
+
3π
8
）（k∈Z）
B、π（
kπ
2
+
π
8
，
kπ
2
+
3π
8
）（k∈Z）
C、
π
2
，（
kπ
2
-
π
8
，
kπ
2
+
π
8
）（k∈Z）
D、
π
4
，（
kπ
2
-
π
8
，
kπ
2
+
π
8
）（k∈Z）
考点：正弦函数的单调性,二倍角的正弦,三角函数的周期性及其求法
专题：三角函数的求值,三角函数的图像与性质
分析：化简解析式可得y=
3
4
-
1
2
sin4x，从而可求周期，由2kπ-
π
2
＜4x＜2kπ+
π
2
可解得单调递减区间．
解答： 解：∵y=sin（
π
6
-2x）cos（
π
6
+2x）=
1
2
[sin
π
3
+sin（-4x）]=
3
4
-
1
2
sin4x，
∴T=
2π
4
=
π
2
，
∴由2kπ-
π
2
＜4x＜2kπ+
π
2
可解得：x∈（
kπ
2
-
π
8
，
kπ
2
+
π
8
）（k∈Z），
故选：C．
点评：本题主要考察了正弦函数的单调性，三角函数的周期性及其求法，属于基础题．
练习册系列答案
相关题目
△ABC中，内角A、B、C的对边分别为a、b、c
（1）若△ABC面积S△ABC=
3
2
，c=2，A=60°，求a，b的值；
（2）若a=c•cosB，且b=c•sinA，试判断△ABC的形状．
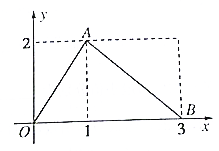函数y=f（x）的图象是如图所示的折线段OAB，已知点A坐标为（1，2）点B的坐标为（3，0），若P（x，y）是函数g（x）=f（x）（x-1）图象上的动点，则x+y的最大值为（　　）
A、
13
4
B、2
C、
7
4
D、4
在等比数列{an}中，T1=a1a2…a100=25，T2=a101a102…a200=75，则T3=a201a202…a300=
．
将函数y=sin（2x+
π
4
）图象上的所有点向左平移
π
4
个单位，得到的图象的函数解析式是（　　）
A、y=sin（2x+
3π
4
）
B、y=sin（2x+
π
2
）
C、y=sin（2x-
π
4
）
D、y=sin2x
已知函数f（x）=
(1-2a)x+5(x≤12)
ax-13(x＞12)
，若数列{an}满足an=f（n）（n∈N*），且{an}是递减数列，则实数a的取值范围是（　　）
A、（
1
2
，1）
B、（
1
2
，
3
4
）
C、（
1
2
，
2
3
）
D、（
3
4
，1）
设{an}是等差数列，Sn是其前n项和，若S2≤3，S3≥6，则S4的最小值为
 
．
若sinx-sin（
3π
2
-x）=
2
，则tanx+
1
tan(x-π)
的值是（　　）
A、2B、-1C、1D、2
点（1，2）到直线y=2x+1的距离为（　　）
A、
5
5
B、
2
5
5
C、
5
D、2
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网