题目内容
19.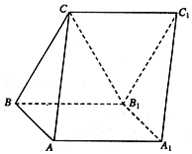 如图,三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.(I)求证:平面AA1B1B⊥平面BB1C1C;
(II)求三棱锥A-B1CC1体积.
分析 (I)证AB垂直于平面内的两条相交直线,再由线面垂直⇒面面垂直;
(II)直接利用体积公式求得三棱锥A-B1CC1体积.
解答 (Ⅰ)证明:由侧面ABB1A1为正方形,知AB⊥BB1.
又AB⊥B1C,BB1∩B1C=B1,所以AB⊥平面BB1C1C,
又AB?平面ABB1A1,所以平面ABB1A1⊥BB1C1C.…(4分)
(Ⅱ)解:由题意,三棱锥A-B1CC1体积=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{2}^{2}×2$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查面面垂直的判定及空间几何体的体积,考查学生分析解决问题的能力,正确运用线面垂直的判定是关键.

练习册系列答案
相关题目
9.函数y=log3x的反函数是( )
| A. | y=-log3x | B. | y=3-x | C. | y=3x | D. | y=-3x |
4.命题“?x∈R,2x+x2≤1”的否定是( )
| A. | ?x∈R,2x+x2>1 | B. | ?x∈R,2x+x2≥1 | C. | ?x∈R,2x+x2>1 | D. | ?x∈R,2x+x2≥1 |
11.不等式$\frac{3x-1}{2-x}≤1$的解集是( )
| A. | {x|$\frac{3}{4}$≤x≤2} | B. | {x|$\frac{3}{4}$≤x<2} | C. | {x|x<2} | D. | {x|x>2或x≤$\frac{3}{4}$} |
8.在复平面内,复数2-i(i是虚数单位)的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |