题目内容
4.已知函数f(x)=x2+2(a-1)x+b在区间(-∞,4]上递减,则a的取值范围是( )| A. | [-3,+∞) | B. | (-∞,-3] | C. | (-∞,5] | D. | [3,+∞) |
分析 由f(x)在区间(-∞,4]上递减知:(-∞,4]为f(x)减区间的子集,由此得不等式,解出即可.
解答 解:f(x)的单调减区间为:(-∞,1-a],
又f(x)在区间(-∞,4]上递减,
所以(-∞,4]⊆(-∞,1-a],则4≤1-a,解得a≤-3,
所以a的取值范围是(-∞,-3],
故选:B.
点评 本题考查二次函数的单调性,属基础题,若函数f(x)在区间(a,b)上递增,则(a,b)为f(x)增区间的子集.

练习册系列答案
相关题目
15.某空间几何体的三视图及其尺寸如图所示,则该几何体的表面积是( )
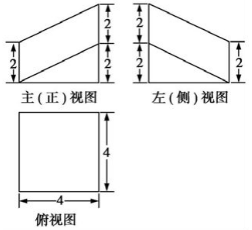

| A. | 32+8$\sqrt{6}$ | B. | 48+8$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 44+8$\sqrt{6}$ |
9.函数y=log3x的反函数是( )
| A. | y=-log3x | B. | y=3-x | C. | y=3x | D. | y=-3x |
13.下列说法正确的是( )
| A. | 若“p或q”为真,则“p且q”也为真 | |
| B. | 命题“若x=2,则x2-5x+6=0”的否命题是“若x=2,则x2-5x+6≠0” | |
| C. | 已知a,b∈R,命题“若a>b,则|a|>|b|”的逆否命题是真命题 | |
| D. | 已知a,b,m∈R,命题“若am2<bm2,则a<b”为真命题 |