题目内容
解二元一次方程组:
.
|
考点:组合及组合数公式
专题:排列组合
分析:由组合数的特点,验证可得只有当r=2,n=6时符合题意.
解答:
解:由题意可知n=3r,r为正整数,
当r=1时,可得n=3,2r•
=6,不合题意;
当r=2时,可得n=6,2r•
=60,符合题意;
当r≥3时,可推出
不是整数,不合题意;
综上可得
.
当r=1时,可得n=3,2r•
| C | r n |
当r=2时,可得n=6,2r•
| C | r n |
当r≥3时,可推出
| C | r n |
综上可得
|
点评:本题考查组合数公式,涉及整数的特点的应用,验证是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则以下判断正确的是( )
| A、f(2013)>e2013f(0) |
| B、f(2013)<e2013f(0) |
| C、f(2013)=e2013f(0) |
| D、f(2013)与e2013f(0)大小无法确定 |
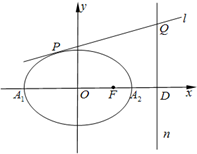 如图,已知椭圆
如图,已知椭圆