题目内容
若有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计,排列组合
分析:先求出2位老师,2位学生站成一排合影,没有任何要求的站法,再求出每位老师都不站在两端的站法,根据古典概型的概率公式可得.
解答:
解:2位老师,2位学生站成一排合影,没有任何要求的排列是
=24种,
每位老师都不站在两端,则两端只能是2名学生站,有
•
=4种,
根据古典概型的概率公式可得,有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是P=
=
,
故选:B.
| A | 4 4 |
每位老师都不站在两端,则两端只能是2名学生站,有
| A | 2 2 |
| A | 2 2 |
根据古典概型的概率公式可得,有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是P=
| 4 |
| 24 |
| 1 |
| 6 |
故选:B.
点评:本题主要考查了古典概型的概率问题,关键是利用排列组合求出基本事件,属于基础题.

练习册系列答案
相关题目
用小立方块搭一个几何体,使它的正视图和俯视图如图所示,则它需要的小立方块的个数最多是( )
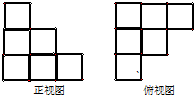

| A、12 | B、13 | C、14 | D、15 |
函数f(x)=1-|1-2x|,x∈[0,1],函数g(x)=x2-2x+1,x∈[0,1],定义函数F(x)=
那么方程F(x)•2x=1的实根的个数是( )
|
| A、0个 | B、1个 | C、2个 | D、3个 |
函数f(x)与g(x)=(
)x的图象关于直线y=x对称,则f(4x-x2)的单调递增区间为( )
| 1 |
| 2 |
| A、(-∞,2) |
| B、(0,2) |
| C、(2,4) |
| D、(2,+∞) |
给出性质:①最小正周期为π;②图象关于直线x=
对称,则下列四个函数中,同时具有性质①②的是( )
| π |
| 6 |
A、y=sin(2x+
| ||
B、y=sin(2x+
| ||
C、y=sin(2x-
| ||
D、y=sin(x+
|