题目内容
已知平面直角坐标系中，点O为坐标原点，点A（sinx，1），B（cosx，0），C（-sinx，2），点P满足
=
．
（1）求函数f（x）=
•
的对称轴方程；
（2）若
∥
，求以线段OA，OB为邻边的平行四边形的对角线长．
| AB |
| BP |
（1）求函数f（x）=
| BP |
| CA |
（2）若
| OP |
| OC |
考点：三角函数中的恒等变换应用,平面向量的综合题
专题：三角函数的图像与性质,平面向量及应用
分析：（1）化简可得f（x）=
sin（2x+
），即可求对称轴方程；
（2）设点P的坐标为（xp，yp），由
=
，
∥
可得cos2x=
，故可求得|
+
|，|
-
|．
| 2 |
| π |
| 4 |
（2）设点P的坐标为（xp，yp），由
| AB |
| BP |
| OP |
| OC |
| 9 |
| 25 |
| OA |
| OB |
| OA |
| OB |
解答：
解：（1）∵
=
=（cosx-sinx，-1），
=（2sinx，-1），
f（x）=2sinx（cosx-sinx）+1=sin2x+cos2x=
sin（2x+
），
令2x+
=kπ+
，k∈Z，得x=
+
，k∈Z，
所以函数f（x）=
•
的对称轴方程为x=
+
，k∈Z．
（2）设点P的坐标为（xp，yp），则
=（xp-cosx，yp），
∵
=
，∴cosx-sinx=xp-cosx，yp=-1，
∴xp=2cosx-sinx，yp=-1，∴点P的坐标为（2cosx-sinx，-1），
因为
=（-sinx，2）且
∥
，
∴（-1）×（-sinx）=2×（2cosx-sinx），∴
=
，
∵sin2x+cos2x=1，∴cos2x=
，
∴|
+
|=
=
=
=
，
∴|
-
|=
=
=
=
，
故以
，
为邻边的平行四边形的对角线长分别为
，
．
| BP |
| AB |
| CA |
f（x）=2sinx（cosx-sinx）+1=sin2x+cos2x=
| 2 |
| π |
| 4 |
令2x+
| π |
| 4 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 8 |
所以函数f（x）=
| BP |
| CA |
| kπ |
| 2 |
| π |
| 8 |
（2）设点P的坐标为（xp，yp），则
| BP |
∵
| BP |
| AB |
∴xp=2cosx-sinx，yp=-1，∴点P的坐标为（2cosx-sinx，-1），
因为
| OC |
| OP |
| OC |
∴（-1）×（-sinx）=2×（2cosx-sinx），∴
| sinx |
| cosx |
| 4 |
| 3 |
∵sin2x+cos2x=1，∴cos2x=
| 9 |
| 25 |
∴|
| OA |
| OB |
| (sinx+cosx)2+1 |
| 2sinxcosx+2 |
|
| ||
| 5 |
∴|
| OA |
| OB |
| (sinx-cosx)2+1 |
| 2-2sinxcosx |
2-
|
| ||
| 5 |
故以
| OA |
| OB |
| ||
| 5 |
| ||
| 5 |
点评：本题主要考察了三角函数中的恒等变换应用，平面向量的综合应用，属于中档题．
练习册系列答案
相关题目
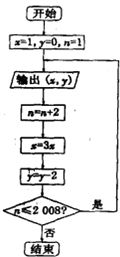已知某算法的程序框图如图，若将输出的（x，y）值一次记为（x1，y1），（x2，y2），（x3，y3）…，（xn，yn）…若程序进行中输出的一个数对是（x，-8），则相应的x值为（ ）| A、80 | B、81 | C、79 | D、78 |
函数f（x）=
的图象大致为（ ）
| 2-x |
| 2-x-1 |
A、 |
B、 |
C、 |
D、 |
若有2位老师，2位学生站成一排合影，则每位老师都不站在两端的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|