题目内容
函数f(x)与g(x)=(
)x的图象关于直线y=x对称,则f(4x-x2)的单调递增区间为( )
| 1 |
| 2 |
| A、(-∞,2) |
| B、(0,2) |
| C、(2,4) |
| D、(2,+∞) |
考点:复合函数的单调性
专题:函数的性质及应用
分析:由条件求得f(4x-x2)=log
(4x-x2),令t=4x-x2>0,求得0<x<4,故f(4x-x2)的定义域为(0,4),本题即求函数f(4x-x2)在(0,4)上的减区间.
再利用二次函数的性质可得函数f(4x-x2)在(0,4)上的减区间.
| 1 |
| 2 |
再利用二次函数的性质可得函数f(4x-x2)在(0,4)上的减区间.
解答:
解:由题意可得函数f(x)与g(x)=(
)x 的互为反函数,故f(x)=log
x,
f(4x-x2)=log
(4x-x2).
令t=4x-x2>0,求得0<x<4,
故f(4x-x2)的定义域为(0,4),
个本题即求函数f(4x-x2)在(0,4)上的减区间.
再利用二次函数的性质可得函数f(4x-x2)在(0,4)上的减区间为(2,4),
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
f(4x-x2)=log
| 1 |
| 2 |
令t=4x-x2>0,求得0<x<4,
故f(4x-x2)的定义域为(0,4),
个本题即求函数f(4x-x2)在(0,4)上的减区间.
再利用二次函数的性质可得函数f(4x-x2)在(0,4)上的减区间为(2,4),
故选:C.
点评:本题主要考查复合函数的单调性,对数函数、二次函数的性质,函数与它的反函数图象间的关系,体现了转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆C1、C2的离心率分别为e1、e2,若椭圆C1比C2更圆,则e1与e2的大小关系正确的是( )
| A、e1<e2 |
| B、e1=e2 |
| C、e1>e2 |
| D、e1、e2大小不确定 |
若有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
方程
-
=1表示椭圆,则α的取值范围是( )
| x2 |
| 3 |
| y2 | ||
sin(2α+
|
A、
| ||||
B、
| ||||
C、kπ+
| ||||
D、2kπ+
|
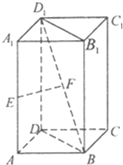 如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.
如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.